Bifurkationen in Morse-Smale-Systemen
Gegeben sei auf 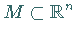 ein von einer Differentialgleichung oder einer Abbildung
erzeugtes dynamisches System
ein von einer Differentialgleichung oder einer Abbildung
erzeugtes dynamisches System 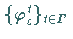 ,
das
zusätzlich von einem Parameter
,
das
zusätzlich von einem Parameter 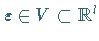 abhängt.
Jede Änderung der topologischen Struktur des Phasenporträts des dynamischen Systems
bei kleiner Änderung des Parameters heißt Bifurkation .
Der Parameter
abhängt.
Jede Änderung der topologischen Struktur des Phasenporträts des dynamischen Systems
bei kleiner Änderung des Parameters heißt Bifurkation .
Der Parameter 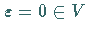 heißt Bifurkationswert , wenn in jeder
Umgebung von
heißt Bifurkationswert , wenn in jeder
Umgebung von 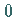 Parameterwerte
Parameterwerte 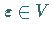 existieren, so daß die
dynamischen Systeme
existieren, so daß die
dynamischen Systeme 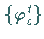 und
und 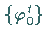 auf
auf 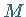 topologisch
nicht äquivalent bzw. nicht konjugiert sind.
Die kleinste Dimension eines Parameterraumes, bei der eine Bifurkation beobachtbar ist,
heißt Kodimension der Bifurkation.
topologisch
nicht äquivalent bzw. nicht konjugiert sind.
Die kleinste Dimension eines Parameterraumes, bei der eine Bifurkation beobachtbar ist,
heißt Kodimension der Bifurkation.
Man unterscheidet lokale Bifurkationen, die nahe einzelner Orbits des dynamischen
Systems ablaufen, und globale Bifurkationen, die sofort einen großen Teil des
Phasenraumes betreffen.