Themen dieser Seite
Spitzen-Bifurkation
Gegeben sei die Differentialgleichung (17.53) mit 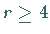 und
und 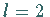 .
Die JACOBI-Matrix
.
Die JACOBI-Matrix 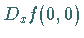 habe den Eigenwert
habe den Eigenwert 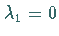 und
und 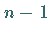 Eigenwerte
Eigenwerte 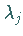 mit Re
mit Re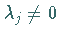 .
Für die reduzierte Differentialgleichung (17.55) gelte
.
Für die reduzierte Differentialgleichung (17.55) gelte
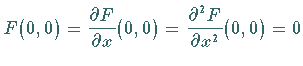 und
und 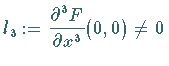 .
Die TAYLOR-Zerlegung von
.
Die TAYLOR-Zerlegung von 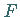 nahe
nahe 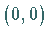 führt auf die verkürzte Normalform
(ohne Glieder höherer Ordnung, s. Lit. 17.1)
führt auf die verkürzte Normalform
(ohne Glieder höherer Ordnung, s. Lit. 17.1)
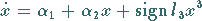 |
(17.62) |
mit den Parametern 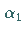 und
und 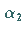 .
Die Menge
.
Die Menge
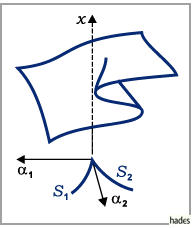
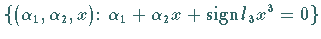 stellt im erweiterten Phasenraum eine Fläche dar und wird Falte genannt
(s. Abbildung).
stellt im erweiterten Phasenraum eine Fläche dar und wird Falte genannt
(s. Abbildung).
Im weiteren sei 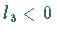 .
Die nicht hyperbolischen Ruhelagen von (17.62) werden durch das Gleichungssystem
.
Die nicht hyperbolischen Ruhelagen von (17.62) werden durch das Gleichungssystem
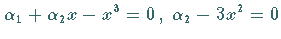 definiert und liegen auf den
Kurven
definiert und liegen auf den
Kurven 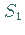 und
und 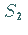 ,
die durch die Menge
,
die durch die Menge
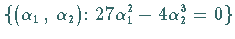 bestimmt
werden und zusammen eine Spitze ( cusp ) bilden (s. linke Abbildung.).
bestimmt
werden und zusammen eine Spitze ( cusp ) bilden (s. linke Abbildung.).
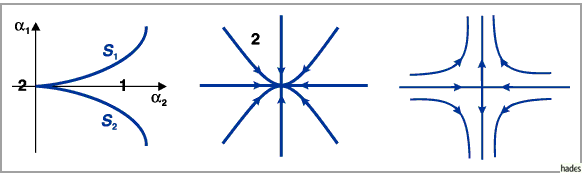
Bei 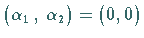 ist die Ruhelage
ist die Ruhelage 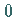 von (17.62) stabil.
Das Phasenporträt von (17.53) nahe
von (17.62) stabil.
Das Phasenporträt von (17.53) nahe 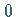 ,
z.B. für
,
z.B. für 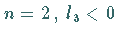 und
und 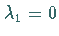 ist für
ist für 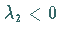 ein dreifach zusammengesetzter
Knoten (s. mittlere Abbildung) und für
ein dreifach zusammengesetzter
Knoten (s. mittlere Abbildung) und für 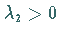 ein dreifach
zusammengesetzter Sattel (s. rechte Abbildung) (s. auch Lit. 17.13).
ein dreifach
zusammengesetzter Sattel (s. rechte Abbildung) (s. auch Lit. 17.13).
Beim Übergang von 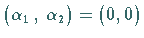 in das Innere des Gebietes 1
(s. linke Abbildung) spaltet sich die nicht hyperbolische Ruhelage
in das Innere des Gebietes 1
(s. linke Abbildung) spaltet sich die nicht hyperbolische Ruhelage 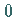 von (17.53)
vom Typ eines zusammengesetzten Knotens in drei hyperbolische Ruhelagen (zwei stabile
Knoten und ein Sattel) auf ( superkritische Gabel-Bifurkation ).
Im Falle des zweidimensionalen Phasenraumes von (17.53) sind die Phasenporträts
in der mittleren und rechten Abbildung zu sehen.
von (17.53)
vom Typ eines zusammengesetzten Knotens in drei hyperbolische Ruhelagen (zwei stabile
Knoten und ein Sattel) auf ( superkritische Gabel-Bifurkation ).
Im Falle des zweidimensionalen Phasenraumes von (17.53) sind die Phasenporträts
in der mittleren und rechten Abbildung zu sehen.
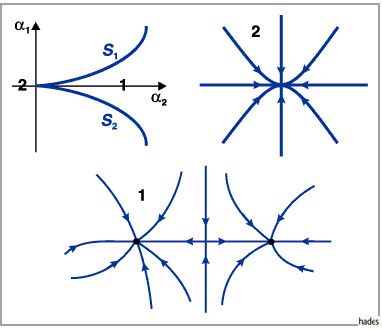
Beim Durchqueren des Parameterpaares von 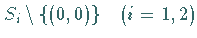 aus
1 in 2 bildet sich eine zweifach zusammengesetzte Ruhelage vom Sattelknoten-Typ, die sich
anschließend aufhebt.
Eine stabile hyperbolische Ruhelage verbleibt.
Für (17.53) gelte
aus
1 in 2 bildet sich eine zweifach zusammengesetzte Ruhelage vom Sattelknoten-Typ, die sich
anschließend aufhebt.
Eine stabile hyperbolische Ruhelage verbleibt.
Für (17.53) gelte 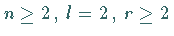 ,
und die Matrix
,
und die Matrix
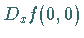 habe die beiden Eigenwerte
habe die beiden Eigenwerte 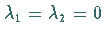 und
und 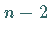 Eigenwerte
Eigenwerte
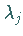 mit Re
mit Re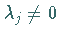 .
Die reduzierte zweidimensionale Differentialgleichung (17.55) sei topologisch
äquivalent zum ebenen System
.
Die reduzierte zweidimensionale Differentialgleichung (17.55) sei topologisch
äquivalent zum ebenen System
 |
(17.63) |
Dann findet auf der Kurve
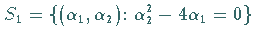 eine Sattelknoten-Bifurkation statt.
Auf
eine Sattelknoten-Bifurkation statt.
Auf 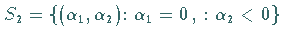 entsteht beim Übergang aus dem Gebiet
entsteht beim Übergang aus dem Gebiet 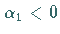 in das Gebiet
in das Gebiet 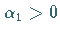 durch eine HOPF-Bifurkation ein stabiler Grenzzyklus und auf
durch eine HOPF-Bifurkation ein stabiler Grenzzyklus und auf
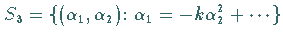
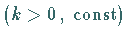 existiert für das Ausgangssystem eine Separatrixschleife
(s. Abbildung), die im Gebiet 3 in einen stabilen Grenzzyklus bifurkiert
(s. Lit. 17.1, 17.17).
existiert für das Ausgangssystem eine Separatrixschleife
(s. Abbildung), die im Gebiet 3 in einen stabilen Grenzzyklus bifurkiert
(s. Lit. 17.1, 17.17).

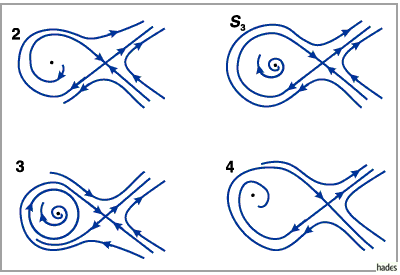
Diese Bifurkation ist von globaler Natur und wird als Entstehung eines einzigen
periodischen Orbits aus dem homoklinen Orbit eines Sattels oder Auflösung
einer Separatrixschleife bezeichnet.
Für (17.53) seien die Voraussetzungen der HOPF-Bifurkation mit
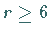 erfüllt und die zweidimensionale reduzierte Differentialgleichung habe
nach einer Koordinatentransformation in Polarkoordinaten die Normalform
erfüllt und die zweidimensionale reduzierte Differentialgleichung habe
nach einer Koordinatentransformation in Polarkoordinaten die Normalform
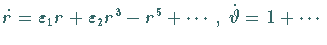 .
Das Bifurkationsdiagramm (s. Abbildung) dieses Systems enthält die Linie
.
Das Bifurkationsdiagramm (s. Abbildung) dieses Systems enthält die Linie
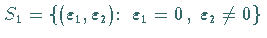 ,
deren Punkte HOPF-Bifurkationen repräsentieren
(s. Lit. 17.1).
,
deren Punkte HOPF-Bifurkationen repräsentieren
(s. Lit. 17.1).
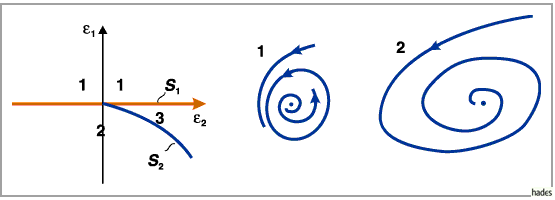
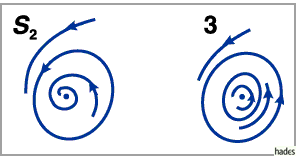
Im Gebiet 3 existieren zwei periodische Orbits, von denen einer stabil, der andere
instabil ist.
Auf der Kurve
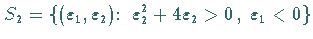 verschmelzen diese beiden nicht hyperbolischen Zyklen in einen zusammengesetzten Zyklus,
der im Gebiet 2 verschwindet.
verschmelzen diese beiden nicht hyperbolischen Zyklen in einen zusammengesetzten Zyklus,
der im Gebiet 2 verschwindet.
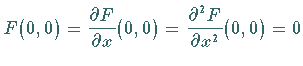 und
und 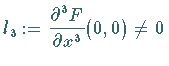 .
Die TAYLOR-Zerlegung von
.
Die TAYLOR-Zerlegung von ![]() eine Sattelknoten-Bifurkation statt.
Auf
eine Sattelknoten-Bifurkation statt.
Auf ![]() entsteht beim Übergang aus dem Gebiet
entsteht beim Übergang aus dem Gebiet ![]() in das Gebiet
in das Gebiet ![]() durch eine HOPF-Bifurkation ein stabiler Grenzzyklus und auf
durch eine HOPF-Bifurkation ein stabiler Grenzzyklus und auf
![]()
![]() existiert für das Ausgangssystem eine Separatrixschleife
(s. Abbildung), die im Gebiet 3 in einen stabilen Grenzzyklus bifurkiert
(s. Lit. 17.1, 17.17).
existiert für das Ausgangssystem eine Separatrixschleife
(s. Abbildung), die im Gebiet 3 in einen stabilen Grenzzyklus bifurkiert
(s. Lit. 17.1, 17.17).