|
|
|
|
und
.
Betrachtet wird ein periodischer Orbit 
von (17.53) bei
mit den Multiplikatoren
und 
.
Das Bifurkationsverhalten der POINCARÉ-Abbildung nahe 
wird durch die
eindimensionale Abbildung (17.66) mit 
beschrieben,
von der die Normalform
von (17.68) ist für kleine 
stabil und
für 
instabil.
Die zweite iterierte Abbildung 
hat bei
außer
noch die beiden stabilen Fixpunkte 
,
die
keine Fixpunkte von 
sind.
Demzufolge müssen sie Punkte der Periode 2 von (17.68) sein.
Allgemein formuliert, kommt es in einer 
-Abbildung (17.66) zur Entstehung
eines zweiperiodischen Orbits bei 
,
wenn folgende Bedingungen
erfüllt sind (s. Lit. 17.2):
 |
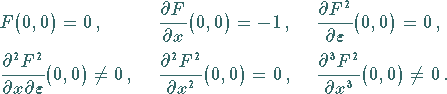(17.69) |
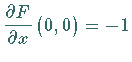auch
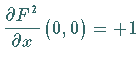ist, sind damit für die Abbildung
die Bedingungen für eine Gabel-Bifurkation formuliert.
Die Eigenschaften der Abbildung (17.68) implizieren für die
Differentialgleichung (17.53), daß sich bei 
von
ein stabiler periodischer Orbit 
mit etwa doppelter Periode
abspaltet ( Periodenverdopplung ), wobei
seine Stabilität verliert
(s. Abbildung).
| Beispiel | |
|
Die logistische Abbildung | |
hat (17.70) die Ruhelage
mit dem
Einzugsgebiet 
.
Für 
besitzt (17.70) die instabile Ruhelage
und die stabile Ruhelage 
,
wobei letztere das Einzugsgebiet
besitzt.
Bei 
wird die Ruhelage 
instabil und zerfällt in
einen stabilen 2periodischen Orbit.
Beim Wert 
wird auch der 2periodische Orbit instabil und durch
einen stabilen 
-periodischen Orbit ersetzt.
Die Periodenverdopplung setzt sich fort, und es entstehen stabile 
-periodische
Orbits bei 
.
Numerische Untersuchungen belegen für 
die Konvergenz
.
Bei 
liegt ein Attraktor 
vor, der
FEIGENBAUM- Attraktor , der die Struktur einer CANTOR-ähnlichen Menge
hat.
In beliebiger Nähe des Attraktors liegen Punkte, die nicht in den Attraktor, sondern
auf instabile periodische Orbits iteriert werden.
Der Attraktor
hat dichte Orbits und eine HAUSDORFF-Dimension
.
Andererseits liegt keine sensitive Abhängigkeit von den Anfangszuständen vor.
Im Bereich 
existiert eine Parametermenge 
mit positivem
LEBESGUE-Maß, so daß für 
das System (17.70)
einen chaotischen Attraktor positiven Maßes besitzt.
Die Menge
ist von Fenstern durchsetzt, in denen Periodenverdopplung auftritt.
Das Bifurkationsverhalten der logistischen Abbildung ist auch in einer Klasse von
unimodalen Abbildungen , d.h. von Abbildungen des Intervalls 
in sich, die in
ein einfaches Maximum besitzen, zu finden.
Obwohl die Parameterwerte 
,
bei denen Periodenverdopplung auftritt, für
verschiedene solche unimodale Abbildungen sich voneinander unterscheiden, ist die
Konvergenzrate, mit der diese Parameter gegen den jeweiligen Wert 
streben,
gleich:
,
wobei 
die FEIGENBAUM-Konstante ist (
hängt von der konkreten Abbildung ab).
Gleich sind auch die HAUSDORFF-Dimensionen der Attraktoren
bei
|
|
ist für
durch 
,
d.h. durch das
diskrete dynamische System
