Bifurkation eines zweifach zusammengesetzten semistabilen periodischen Orbits
Gegeben sei das System (17.53) mit 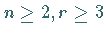 und
und
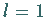 .
Das System (17.53) habe bei
.
Das System (17.53) habe bei  den periodischen
Orbit
den periodischen
Orbit 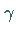 mit den Multiplikatoren
mit den Multiplikatoren
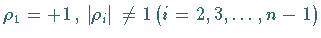 und
und 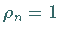 .
.
Nach dem Satz über die
Zentrumsmannigfaltigkeit für Abbildungen werden
Bifurkationen in der POINCARÉ-Abbildung (17.64)
durch die eindimensionale reduzierte Abbildung (17.66) mit 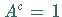 beschrieben.
Wird dabei
beschrieben.
Wird dabei 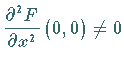 und
und
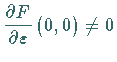 vorausgesetzt, so führt dies
auf die Normalformen
vorausgesetzt, so führt dies
auf die Normalformen
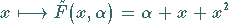 |
(17.67) |
(bei 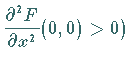 bzw.
bzw.
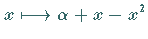 (bei
(bei 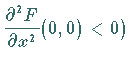 .
Die Iterationsverläufe von (17.67) nahe
.
Die Iterationsverläufe von (17.67) nahe 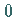 und die zugehörigen
Phasenporträts sind für verschiedene
und die zugehörigen
Phasenporträts sind für verschiedene 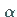 in den folgenden beiden Abbildungen
zu sehen (s. Lit. 17.1).
in den folgenden beiden Abbildungen
zu sehen (s. Lit. 17.1).
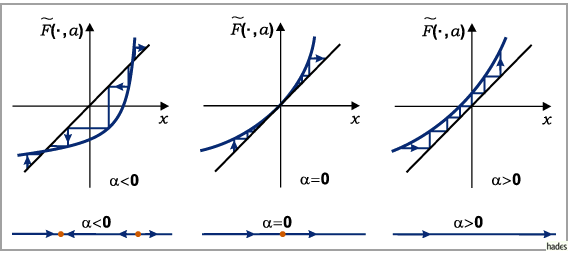
Für 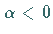 liegen eine stabile und eine instabile Ruhelage nahe
liegen eine stabile und eine instabile Ruhelage nahe 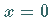 vor,
die für
vor,
die für 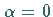 in der instabilen Ruhelage
in der instabilen Ruhelage 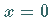 verschmelzen.
Für
verschmelzen.
Für 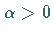 existiert keine Ruhelage nahe
existiert keine Ruhelage nahe  .
Die durch (17.67) beschriebene Bifurkation in (17.66) heißt
subkritische Sattelknoten-Bifurkation für Abbildungen.
.
Die durch (17.67) beschriebene Bifurkation in (17.66) heißt
subkritische Sattelknoten-Bifurkation für Abbildungen.
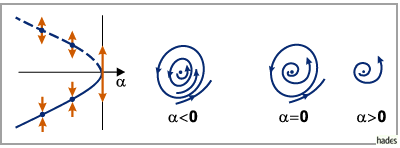
Für die Differentialgleichung (17.53) beschreiben die Eigenschaften der
Abbildung (17.67) die Bifurkation eines zweifach zusammengesetzten
semistabilen periodischen Orbits:
Bei 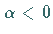 existieren ein stabiler periodischer Orbit
existieren ein stabiler periodischer Orbit 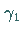 und ein
instabiler periodischer Orbit
und ein
instabiler periodischer Orbit 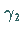 ,
die bei
,
die bei 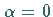 zu einem semistabilen
Orbit
zu einem semistabilen
Orbit 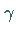 verschmelzen, der sich bei
verschmelzen, der sich bei 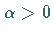 auflöst (s. Abbildung).
auflöst (s. Abbildung).
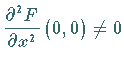 und
und
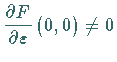 vorausgesetzt, so führt dies
auf die Normalformen
vorausgesetzt, so führt dies
auf die Normalformen
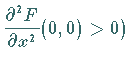 bzw.
bzw.
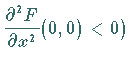 .
Die Iterationsverläufe von (17.67) nahe
.
Die Iterationsverläufe von (17.67) nahe ![]() existieren ein stabiler periodischer Orbit
existieren ein stabiler periodischer Orbit ![]() und ein
instabiler periodischer Orbit
und ein
instabiler periodischer Orbit ![]() ,
die bei
,
die bei ![]() zu einem semistabilen
Orbit
zu einem semistabilen
Orbit ![]() verschmelzen, der sich bei
verschmelzen, der sich bei ![]() auflöst (s. Abbildung).
auflöst (s. Abbildung).