|
|
|
|
,
wobei 
und 
offene Mengen darstellen und 
als 
-mal stetig differenzierbar vorausgesetzt wird.
Die Gleichung (17.53) läßt sich als parameterfreie Differentialgleichung
im Phasenraum 
interpretieren.
Aus dem Satz von PICARD - LINDELÖF und dem Satz über die
und 
eine
lokal eindeutige Lösung 
mit Anfang 
zur Zeit 
besitzt, die bezüglich
und 
dann -mal stetig differenzierbar ist.
Alle Lösungen mögen auf ganz 
existieren.
Es wird weiter vorausgesetzt, daß System (17.53) bei 
die Ruhelage 
besitzt, d.h., es gelte 
.
Es seien 
die Eigenwerte von
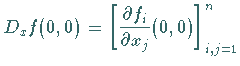mit
Re
.
Außerdem habe 
genau 
Eigenwerte mit negativem und 
Eigenwerte mit positivem Realteil.
Nach dem Satz über die Zentrumsmannigfaltigkeit für Differentialgleichungen
( Satz von SHOSHITAISHVILI) (s. Lit. 17.12) ist die
Differentialgleichung (17.53) für
mit hinreichend kleiner Norm
in einer Umgebung von 
topologisch äquivalent zu einem System
und 
,
wobei 
eine Matrix vom Typ 
ist,
die
als Eigenwerte hat, und 
eine 
-Funktion mit
sowie 
darstellt.
Aus der Darstellung (17.54) folgt, daß Bifurkationen von (17.53) in
einer Umgebung von
ausschließlich durch die Differentialgleichung
von (17.54)
reduzierte Differentialgleichung dar.
Die reduzierte Differentialgleichung (17.55) kann oft durch eine nichtlineare parameterabhängige Koordinatentransformation, die die topologische Struktur ihres Phasenporträts nahe der untersuchten Ruhelage nicht ändert, auf eine relativ einfache Form (z.B. mit Polynomen auf der rechten Seite) gebracht werden, die Normalform heißt. Eine Normalform läßt sich nicht eindeutig bestimmen; in der Regel wird eine Bifurkation durch unterschiedliche Normalformen äquivalent beschrieben.
|
|
