|
|
|
|
Nach dem Satz über die Zentrumsmannigfaltigkeit ergibt
sich in der vorliegenden Situation eine zweidimensionale reduzierte ![]() -Abbildung
-Abbildung
Hat die JACOBI-Matrix ![]() für alle
für alle ![]() nahe
nahe ![]() die
konjugiert komplexen Eigenwerte
die
konjugiert komplexen Eigenwerte ![]() und
und ![]() mit
mit ![]() ,
ist
,
ist
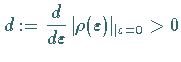 und
ist
und
ist ![]() für
für ![]() keine
keine ![]() -te Wurzel aus
-te Wurzel aus ![]() ,
so läßt sich
(17.61) durch eine glatte
,
so läßt sich
(17.61) durch eine glatte ![]() -abhängige Koordinatentransformation
auf die Form
-abhängige Koordinatentransformation
auf die Form
![]() bringen
(
bringen
(![]() LANDAU-Symbol), wobei
LANDAU-Symbol), wobei ![]() in Polarkoordinaten
durch
in Polarkoordinaten
durch
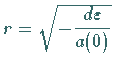 ,
der invariant unter der Abbildung
(17.72) und asymptotisch stabil ist (s. linke Abbildung).
,
der invariant unter der Abbildung
(17.72) und asymptotisch stabil ist (s. linke Abbildung).
| Beispiel | |
|
In der Abbildung (17.71), gegeben durch | |
Bezogen auf die Differentialgleichung (17.53) bedeutet die Existenz einer
geschlossenen invarianten Kurve der Abbildung (17.71), daß bei ![]() der periodische Orbit
der periodische Orbit ![]() instabil wird und sich bei
instabil wird und sich bei ![]() ein
bezüglich (17.53) invarianter stabiler Torus abspaltet (s. Abbildung).
ein
bezüglich (17.53) invarianter stabiler Torus abspaltet (s. Abbildung).
|
|
|