Satz über die Zentrumsmannigfaltigkeit für Abbildungen
Gegeben sei ein periodischer Orbit 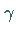 von (17.53) bei
von (17.53) bei  mit den Multiplikatoren
mit den Multiplikatoren 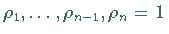 .
Eine Bifurkation nahe
.
Eine Bifurkation nahe 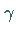 ist möglich, wenn bei Änderung von
ist möglich, wenn bei Änderung von 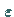 mindestens einer der Multiplikatoren auf den komplexen Einheitskreis trifft.
Die Verwendung einer zu
mindestens einer der Multiplikatoren auf den komplexen Einheitskreis trifft.
Die Verwendung einer zu 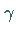 transversalen Fläche führt auf eine
parameterabhängige POINCARÉ-Abbildung
transversalen Fläche führt auf eine
parameterabhängige POINCARÉ-Abbildung
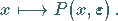 |
(17.64) |
Dabei sei 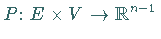 ,
wobei
,
wobei  und
und
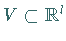 offene Mengen sind, eine
offene Mengen sind, eine 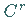 -Abbildung, wobei die Abbildung
-Abbildung, wobei die Abbildung
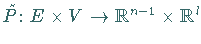 mit
mit
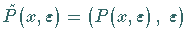 sogar ein
sogar ein
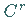 -Diffeomorphismus sei.
Es sei weiter
-Diffeomorphismus sei.
Es sei weiter 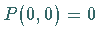 und die JACOBI-Matrix
und die JACOBI-Matrix 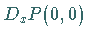 habe
habe 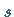 Eigenwerte
Eigenwerte 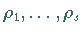 mit
mit
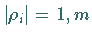 Eigenwerte
Eigenwerte 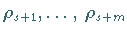 mit
mit 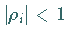 und
und 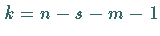 Eigenwerte
Eigenwerte 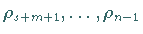 mit
mit
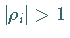 .
Dann ist nach dem Satz über die Zentrumsmannigfaltigkeit für Abbildungen
(s. Lit. 17.12)
.
Dann ist nach dem Satz über die Zentrumsmannigfaltigkeit für Abbildungen
(s. Lit. 17.12) 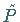 nahe
nahe 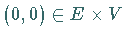 topologisch
konjugiert zur Abbildung
topologisch
konjugiert zur Abbildung
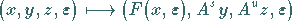 |
(17.65) |
nahe 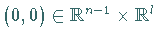 mit
mit 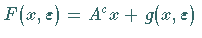 .
Dabei ist
.
Dabei ist 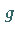 eine
eine 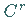 -differenzierbare Abbildung, die den Bedingungen
-differenzierbare Abbildung, die den Bedingungen 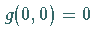 und
und 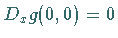 genügt.
Außerdem sind
genügt.
Außerdem sind 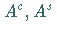 bzw.
bzw. 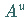 Matrizen vom Typ
Matrizen vom Typ 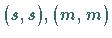 bzw.
bzw. 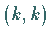 mit Eigenwerten auf, innerhalb bzw. außerhalb des Einheitskreises.
mit Eigenwerten auf, innerhalb bzw. außerhalb des Einheitskreises.
Aus (17.65) folgt, daß Bifurkationen von (17.64) nahe 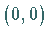 ausschließlich durch die reduzierte Abbildung
ausschließlich durch die reduzierte Abbildung
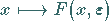 |
(17.66) |
auf der lokalen Zentrumsmannigfaltigkeit
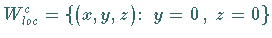 beschrieben werden.
beschrieben werden.
![]() ausschließlich durch die reduzierte Abbildung
ausschließlich durch die reduzierte Abbildung