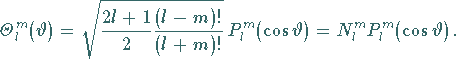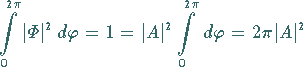Themen dieser Seite
Problemstellung
Das betrachtete Teilchen wird durch ein radialsymmetrisches Potential 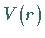 gezwungen,
sich ausschließlich auf Kugeloberflächenbahnen mit dem konstantem Radius
gezwungen,
sich ausschließlich auf Kugeloberflächenbahnen mit dem konstantem Radius
 zu bewegen.
Dieses Modell reproduziert die Bewegung eines Elektrons unter der elektrostatischen
Anziehung eines positiv geladenen Kerns.
Da es sich um ein kugelsymmetrisches Problem handelt, ist die Benutzung von
Kugelkoordinaten zweckmäßig (s. Abbildung).
zu bewegen.
Dieses Modell reproduziert die Bewegung eines Elektrons unter der elektrostatischen
Anziehung eines positiv geladenen Kerns.
Da es sich um ein kugelsymmetrisches Problem handelt, ist die Benutzung von
Kugelkoordinaten zweckmäßig (s. Abbildung).
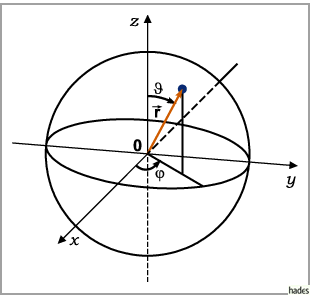
Es gelten dann die Beziehungen
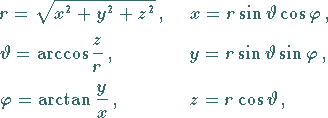 |
(9.116a) |
wobei 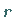 der Radiusvektor ist,
der Radiusvektor ist, 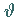 der Winkel zwischen Radiusvektor und
der Winkel zwischen Radiusvektor und
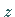 -Achse (Polarwinkel) und
-Achse (Polarwinkel) und 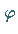 der Winkel zwischen der Projektion des
Radiusvektors auf die
der Winkel zwischen der Projektion des
Radiusvektors auf die 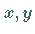 -Ebene und der
-Ebene und der 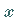 -Achse (Azimutalwinkel).
Für den LAPLACE-Operator ergibt sich
-Achse (Azimutalwinkel).
Für den LAPLACE-Operator ergibt sich
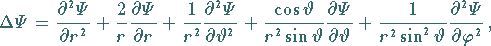 |
(9.116b) |
so daß die zeitunabhängige SCHRÖDINGER-Gleichung dieses raumfreien
starren Rotators lautet:
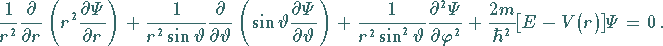 |
(9.116c) |
Lösungsansätze
Eine Lösung wird mit dem Ansatz
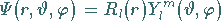 |
(9.117a) |
angestrebt, in dem 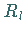 die nur vom Radius
die nur vom Radius 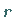 abhängige radiale Wellenfunktion ist
und
abhängige radiale Wellenfunktion ist
und 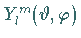 eine nur von den beiden Winkeln abhängige
Wellenfunktion.
Einsetzen von (9.117a) in (9.116c) liefert
eine nur von den beiden Winkeln abhängige
Wellenfunktion.
Einsetzen von (9.117a) in (9.116c) liefert
| |
|
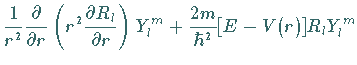 |
|
| |
|
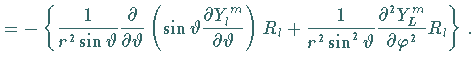 |
(9.117b) |
Division durch 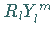 und Multiplikation mit
und Multiplikation mit 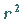 ergibt
ergibt
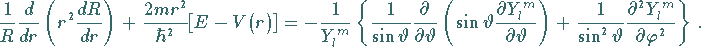 |
(9.117c) |
Diese Gleichung (9.117c) kann nur erfüllt werden, wenn eine
unabhängige Variation der Radiuskoordinate 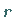 auf der linken Seite der Gleichung und
der Winkelkoordinaten
auf der linken Seite der Gleichung und
der Winkelkoordinaten 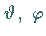 auf der rechten dieselbe
Separationskonstante ergeben, d.h., wenn die Seiten unabhängig voneinander sind und
den gleichen konstanten Wert ergeben.
Aus der partiellen Differentialgleichung ergeben sich dann eine gewöhnliche und eine
partielle Differentialgleichung.
Wird die Separationskonstante praktischerweise gleich
auf der rechten dieselbe
Separationskonstante ergeben, d.h., wenn die Seiten unabhängig voneinander sind und
den gleichen konstanten Wert ergeben.
Aus der partiellen Differentialgleichung ergeben sich dann eine gewöhnliche und eine
partielle Differentialgleichung.
Wird die Separationskonstante praktischerweise gleich 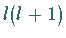 gesetzt, dann erhält
man die nur von
gesetzt, dann erhält
man die nur von 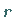 und vom Potential
und vom Potential 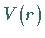 abhängige sogenannte
Radialgleichung :
abhängige sogenannte
Radialgleichung :
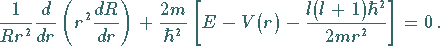 |
(9.117d) |
Der winkelabhängige Anteil wird mit Hilfe des Ansatzes
 |
(9.117e) |
ebenfalls separiert.
Einsetzen von (9.117e) in (9.117c) liefert
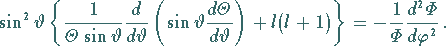 |
(9.117f) |
Bezeichnet man die Separationskonstante zweckmäßigerweise mit 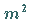 ,
dann lautet
die sogenannte Polargleichung
,
dann lautet
die sogenannte Polargleichung
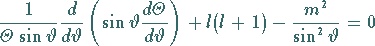 |
(9.117g) |
und die Azimutalgleichung
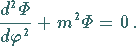 |
(9.117h) |
Beide Gleichungen sind potentialunabhängig, gelten also für jedes zentralsymmetrische
Potential.
An die Lösung (9.117a) sind drei Forderungen zu stellen: Sie soll für
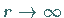 verschwinden, auf der Kugeloberfläche eindeutig sein und sich quadratisch
integrieren lassen.
verschwinden, auf der Kugeloberfläche eindeutig sein und sich quadratisch
integrieren lassen.
Lösung der Radialgleichung
Die Radialgleichung (9.117d) enthält neben dem Potential 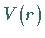 noch die
Separationskonstante
noch die
Separationskonstante 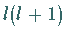 .
Man schreibt deshalb
.
Man schreibt deshalb 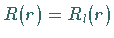 und substituiert
und substituiert
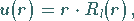 |
(9.118a) |
weil das Quadrat der Funktion 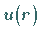 die letztlich gesuchte Aufenthaltswahrscheinlichkeit
die letztlich gesuchte Aufenthaltswahrscheinlichkeit
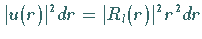 des Teilchens in einer Kugelschale zwischen
des Teilchens in einer Kugelschale zwischen 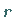 und
und
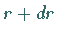 angibt.
Die Substitution führt auf die eindimensionale SCHRÖDINGER-Gleichung
angibt.
Die Substitution führt auf die eindimensionale SCHRÖDINGER-Gleichung
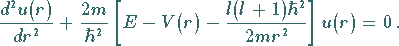 |
(9.118b) |
Diese enthält das effektive Potential
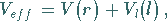 |
(9.118c) |
das aus zwei Anteilen besteht.
Die Rotationsenergie
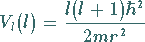 |
(9.118d) |
wird Zentrifugalpotential genannt.
Die physikalische Bedeutung von 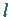 als Bahndrehimpuls-Quantenzahl ergibt sich aus
der Analogiebetrachtung zur klassischen Rotationsenergie
als Bahndrehimpuls-Quantenzahl ergibt sich aus
der Analogiebetrachtung zur klassischen Rotationsenergie
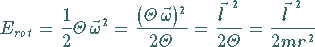 |
(9.118e) |
eines rotierenden Teilchens mit dem Trägheitsmoment 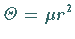 und dem
Bahndrehimpuls
und dem
Bahndrehimpuls 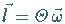 :
:
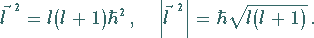 |
(9.118f) |
Die Polargleichung (9.117g), die beide Separationskonstanten 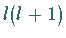 und
und
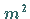 enthält, ist eine LEGENDREsche Differentialgleichung.
Ihre Lösung wird mit
enthält, ist eine LEGENDREsche Differentialgleichung.
Ihre Lösung wird mit 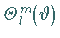 bezeichnet und kann durch einen
Potenzreihenansatz ermittelt werden.
Endliche, eindeutige und stetige Lösungen ergeben sich nur für
bezeichnet und kann durch einen
Potenzreihenansatz ermittelt werden.
Endliche, eindeutige und stetige Lösungen ergeben sich nur für
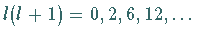 .
Daher gilt für
.
Daher gilt für 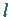 und
und 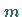 :
:
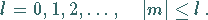 |
(9.119a) |
Somit kann 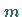 insgesamt die
insgesamt die 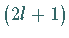 Werte
Werte
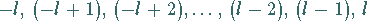 |
(9.119b) |
durchlaufen.
Für 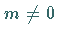 ergeben sich die zugeordneten LEGENDREschen Polynome,
die wie folgt definiert sind:
ergeben sich die zugeordneten LEGENDREschen Polynome,
die wie folgt definiert sind:
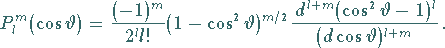 |
(9.119c) |
Als Spezialfall (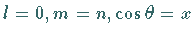 )erhält man die
LEGENDREschen Polynome 1. Art
)erhält man die
LEGENDREschen Polynome 1. Art 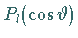 (9.57b) (s. auch Tabelle LEGENDREsche Polynome 1. Art).
Die Normierung führt auf
(9.57b) (s. auch Tabelle LEGENDREsche Polynome 1. Art).
Die Normierung führt auf
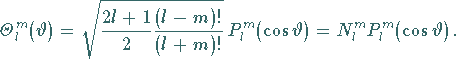 |
(9.119d) |
Lösung der Azimutalgleichung
Da die Teilchenbewegung auf der Kugeloberfläche auch im Falle der physikalischen
Auszeichnung einer Raumrichtung, z.B. durch ein Magnetfeld, unabhängig vom
Azimutalwinkel ist, spezifiziert man die allgemeine Lösung
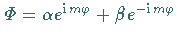 durch die
Festlegung
durch die
Festlegung
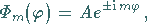 |
(9.120a) |
für die 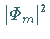 unabhängig von
unabhängig von 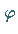 ist.
Aus der Forderung nach Eindeutigkeit
ist.
Aus der Forderung nach Eindeutigkeit
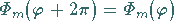 |
(9.120b) |
folgt, daß 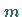 nur die Werte
nur die Werte 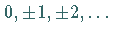 annehmen darf.
annehmen darf.
Aus der Normierung
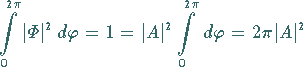 |
(9.120c) |
folgt
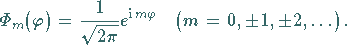 |
(9.120d) |
Die Quantenzahl 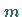 wird magnetische Quantenzahl genannt.
wird magnetische Quantenzahl genannt.
Gesamtlösung für die Winkelabhängigkeit
In Übereinstimmung mit (9.117e) sind die Lösungen für die
Polar- und die Azimutalgleichungen miteinander zu multiplizieren:
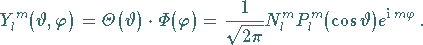 |
(9.121a) |
Die Funktionen 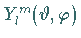 sind die sogenannten
Kugelflächenfunktionen .
sind die sogenannten
Kugelflächenfunktionen .
Wenn der Radiusvektor 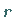 am Koordinatenursprung gespiegelt wird
am Koordinatenursprung gespiegelt wird 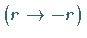 ,
geht
,
geht
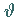 in
in 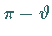 über und
über und 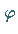 in
in 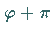 ,
so daß
sich das Vorzeichen von
,
so daß
sich das Vorzeichen von 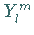 ändern kann:
ändern kann:
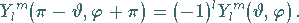 |
(9.121b) |
Daraus ergibt sich die Parität der betrachteten Wellenfunktion zu:
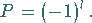 |
(9.122a) |
Parität:
Die Eigenschaft Parität dient der Charakterisierung des Verhaltens der Wellenfunktion
bei Rauminversion 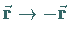 .
Diese Operation wird mit dem Inversions- oder Paritätsoperator
.
Diese Operation wird mit dem Inversions- oder Paritätsoperator 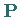 durchgeführt:
durchgeführt:
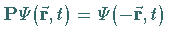 .
Bezeichnet man den Eigenwert des Operators mit
.
Bezeichnet man den Eigenwert des Operators mit 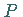 ,
dann muß eine zweimalige
Anwendung von
,
dann muß eine zweimalige
Anwendung von 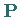 ,
d.h.
,
d.h. 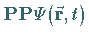 auf
auf
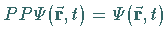 führen, also auf die
ursprüngliche Wellenfunktion.
Daraus folgt:
führen, also auf die
ursprüngliche Wellenfunktion.
Daraus folgt:
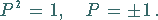 |
(9.122b) |
Man spricht von gerader Wellenfunktion , wenn sie bei Rauminversion ihr
Vorzeichen nicht ändert, von ungerader Wellenfunktion , wenn sie es
ändert.
Die Parität setzt sich aus zwei Faktoren zusammen, der inneren Parität
und der äußeren Parität .
Letztere hängt vom Drehimpuls des beschriebenen Teilchens oder Systems gemäß
(9.122a) ab.
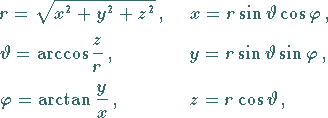
![]() der Radiusvektor ist,
der Radiusvektor ist, ![]() der Winkel zwischen Radiusvektor und
der Winkel zwischen Radiusvektor und
![]() -Achse (Polarwinkel) und
-Achse (Polarwinkel) und ![]() der Winkel zwischen der Projektion des
Radiusvektors auf die
der Winkel zwischen der Projektion des
Radiusvektors auf die ![]() -Ebene und der
-Ebene und der ![]() -Achse (Azimutalwinkel).
Für den LAPLACE-Operator ergibt sich
-Achse (Azimutalwinkel).
Für den LAPLACE-Operator ergibt sich
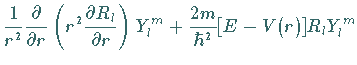
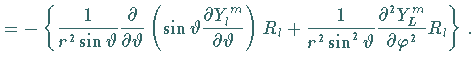
![]() und Multiplikation mit
und Multiplikation mit ![]() ergibt
ergibt
![]() ,
dann lautet
die sogenannte Polargleichung
,
dann lautet
die sogenannte Polargleichung
![]() verschwinden, auf der Kugeloberfläche eindeutig sein und sich quadratisch
integrieren lassen.
verschwinden, auf der Kugeloberfläche eindeutig sein und sich quadratisch
integrieren lassen.
![]() die letztlich gesuchte Aufenthaltswahrscheinlichkeit
die letztlich gesuchte Aufenthaltswahrscheinlichkeit
![]() des Teilchens in einer Kugelschale zwischen
des Teilchens in einer Kugelschale zwischen ![]() und
und
![]() angibt.
Die Substitution führt auf die eindimensionale SCHRÖDINGER-Gleichung
angibt.
Die Substitution führt auf die eindimensionale SCHRÖDINGER-Gleichung
![]() als Bahndrehimpuls-Quantenzahl ergibt sich aus
der Analogiebetrachtung zur klassischen Rotationsenergie
als Bahndrehimpuls-Quantenzahl ergibt sich aus
der Analogiebetrachtung zur klassischen Rotationsenergie
![]() und dem
Bahndrehimpuls
und dem
Bahndrehimpuls ![]() :
: