Themen dieser Seite
Linearer harmonischer Oszillator
Harmonische Schwingungen entstehen, wenn die rücktreibende Kraft im
Oszillator dem HOOKEschen Gesetz 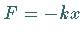 genügt.
Für Schwingungsfrequenz, Schwingungskreisfrequenz und potentielle Energie ergeben sich:
genügt.
Für Schwingungsfrequenz, Schwingungskreisfrequenz und potentielle Energie ergeben sich:
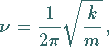 |
(9.123a) |
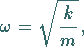 |
(9.123b) |
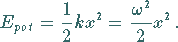 |
(9.123c) |
Durch Einsetzen in (9.112a) erhält die
SCHRÖDINGER-Gleichung die Form:
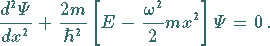 |
(9.124a) |
Mit Hilfe der Substitutionen
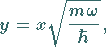 |
(9.124b) |
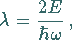 |
(9.124c) |
wobei 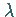 ein Parameter und nicht die Wellenlänge ist, kann
(9.124a) in die einfachere Form der WEBERschen
Differentialgleichung
ein Parameter und nicht die Wellenlänge ist, kann
(9.124a) in die einfachere Form der WEBERschen
Differentialgleichung
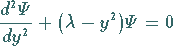 |
(9.124d) |
überführt werden.
Für die WEBERsche Differentialgleichung erhält man mit Hilfe des Ansatzes
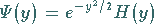 |
(9.125a) |
eine Lösung.
Differentiation führt auf
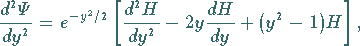 |
(9.125b) |
Einsetzen in die SCHRÖDINGER-Gleichung (9.124d) liefert
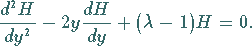 |
(9.125c) |
Eine Lösung wird über den Reihenansatz
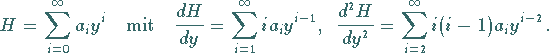 |
(9.126a) |
bestimmt:
Einsetzen von (9.126a) in (9.125c) ergibt
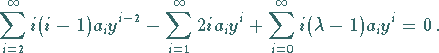 |
(9.126b) |
Durch Vergleich der Koeffizienten von 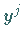 erhält man die Rekursionsformel
erhält man die Rekursionsformel
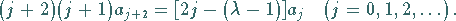 |
(9.126c) |
Die Koeffizienten 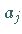 für gerade Potenzen von
für gerade Potenzen von 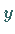 werden auf
werden auf  zurückgeführt,
die Koeffizienten für ungerade Potenzen auf
zurückgeführt,
die Koeffizienten für ungerade Potenzen auf 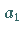 .
Damit sind
.
Damit sind  und
und 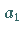 frei wählbar.
frei wählbar.
Physikalische Lösungen
Gesucht ist die Aufenthaltswahrscheinlichkeit des betrachteten Teilchens in den
verschiedenen Zuständen.
Diese wird mit Hilfe einer physikalisch sinnvollen, d.h. normierbaren, für große
Werte von 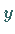 gegen Null gehenden Eigenfunktion und quadratisch integrierbaren
Wellenfunktion
gegen Null gehenden Eigenfunktion und quadratisch integrierbaren
Wellenfunktion 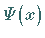 beschrieben.
beschrieben.
Die Exponentialfunktion 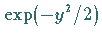 im Ansatz (9.125a)
sorgt dafür, daß die Lösung
im Ansatz (9.125a)
sorgt dafür, daß die Lösung 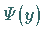 für
für 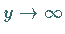 gegen Null
strebt, wenn die Funktion
gegen Null
strebt, wenn die Funktion 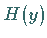 ein Polynom ist.
Daher müssen die Koeffizienten
ein Polynom ist.
Daher müssen die Koeffizienten 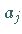 in (9.126a), beginnend von
einem bestimmten
in (9.126a), beginnend von
einem bestimmten  an, für alle
an, für alle 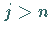 verschwinden:
verschwinden:
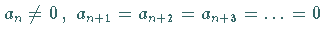 .
Mit
.
Mit 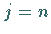 lautet die Rekursionsformel (9.126c) jetzt
lautet die Rekursionsformel (9.126c) jetzt
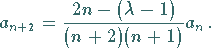 |
(9.127a) |
Für 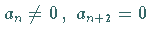 kann sie nur erfüllt werden, wenn
kann sie nur erfüllt werden, wenn
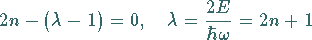 |
(9.127b) |
gesetzt wird.
Somit verschwinden durch die angegebene Wahl von 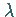 die Koeffizienten
die Koeffizienten
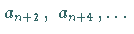 .
Damit auch die Koeffizienten
.
Damit auch die Koeffizienten 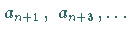 verschwinden, muß
verschwinden, muß
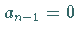 sein.
sein.
Für die spezielle Wahl 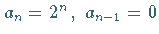 erhält man die
HERMITEschen Polynome der 2. Definitionsgleichung.
Die ersten sechs lauten:
erhält man die
HERMITEschen Polynome der 2. Definitionsgleichung.
Die ersten sechs lauten:
Die Lösung 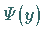 für die Schwingungsquantenzahl
für die Schwingungsquantenzahl  ergibt
sich zu
ergibt
sich zu
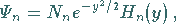 |
(9.128a) |
wobei 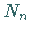 der Normierungsfaktor ist.
Man erhält ihn aus der Normierungsbedingung
der Normierungsfaktor ist.
Man erhält ihn aus der Normierungsbedingung 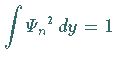 zu
zu
 |
(9.128b) |
Für die Eigenwerte der Schwingungsenergie ergibt sich als
Quantisierungsbedingung aus der Bedingung für den Abbruch der Reihe mit
(9.124c)
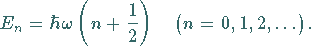 |
(9.128c) |
Das Spektrum der Energiezustände ist äquidistant.
Der Summand 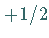 in der Klammer bedeutet, daß der quantenmechanische Oszillator im
Unterschied zum klassischen auch im tiefsten energetischen Zustand mit
in der Klammer bedeutet, daß der quantenmechanische Oszillator im
Unterschied zum klassischen auch im tiefsten energetischen Zustand mit  Energie
besitzt, die Nullpunktsschwingungsenergie .
Energie
besitzt, die Nullpunktsschwingungsenergie .
Die folgende Abbildung zeigt eine graphische Darstellung des äquidistanten Spektrums der
Energiezustände, die zugehörigen Wellenfunktionen 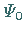 bis
bis 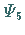 sowie die Funktion der potentiellen Energie (9.123c).
sowie die Funktion der potentiellen Energie (9.123c).
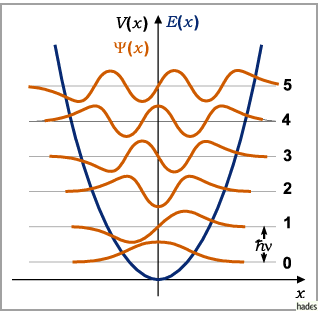
Die Punkte auf der Parabel der potentiellen Energie bezeichnen die Umkehrpunkte des
klassischen Oszillators, die als Amplitude
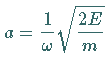 aus der Energie
aus der Energie
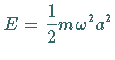 berechnet werden.
Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall
berechnet werden.
Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall 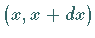 zu
finden, ist durch
zu
finden, ist durch 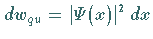 gegeben.
Sie ist auch außerhalb dieser Punkte von Null verschieden.
So liefert z.B.
gegeben.
Sie ist auch außerhalb dieser Punkte von Null verschieden.
So liefert z.B.  ,
also
,
also 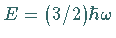 ,
gemäß
,
gemäß
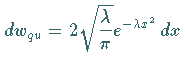 ,
Maxima der Aufenthaltswahrscheinlichkeit bei
,
Maxima der Aufenthaltswahrscheinlichkeit bei
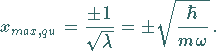 |
(9.128d) |
Für den entsprechenden klassischen Oszillator ergibt sich
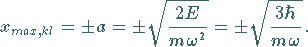 |
(9.128e) |
Die quantenmechanische Verteilungsdichte nähert sich für große Werte der
Quantenzahl  in ihrem Mittelwert der klassischen.
in ihrem Mittelwert der klassischen.
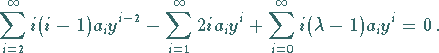
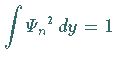 zu
zu
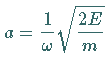 aus der Energie
aus der Energie
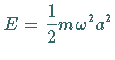 berechnet werden.
Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall
berechnet werden.
Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall 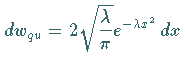 ,
Maxima der Aufenthaltswahrscheinlichkeit bei
,
Maxima der Aufenthaltswahrscheinlichkeit bei