Themen dieser Seite
Besselsche Differentialgleichung
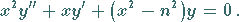 |
(9.52a) |
Die Definierende Gleichung ist in diesem Falle
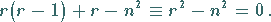 |
(9.52b) |
Daraus folgt 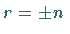 .
Einsetzen von
.
Einsetzen von
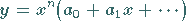 |
(9.52c) |
in diese Gleichung liefert für den zu Null gesetzten Koeffizienten von 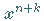 die Bestimmungsgleichung
die Bestimmungsgleichung
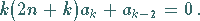 |
(9.52d) |
Für 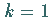 erhält man
erhält man 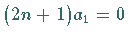 .
Für die Werte
.
Für die Werte 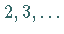 von
von 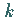 ergibt sich
ergibt sich
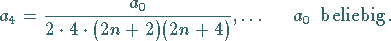 |
(9.52e) |
Bessel- oder Zylinderfunktionen:
Die für 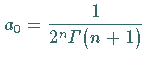 (
(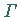 s. Gammafunktion) entstandene Reihe ist eine
partikuläre Lösung der BESSELschen Differentialgleichung
(9.52a) für ganzzahlige
s. Gammafunktion) entstandene Reihe ist eine
partikuläre Lösung der BESSELschen Differentialgleichung
(9.52a) für ganzzahlige 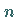 .
Sie definiert die BESSEL- oder Zylinderfunktion
.
Sie definiert die BESSEL- oder Zylinderfunktion  -ter Ordnung
1. Gattung
-ter Ordnung
1. Gattung
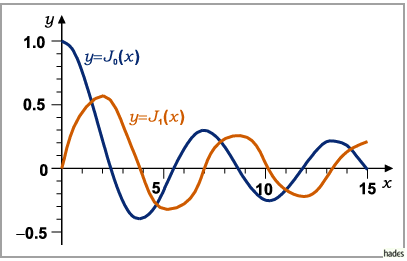
Die Kurvenbilder der Funktionen 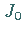 und
und 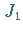 zeigt die folgende Abbildung.
zeigt die folgende Abbildung.
Die allgemeine Lösung der BESSELschen Differentialgleichung für nicht
ganzzahlige  hat die Form
hat die Form
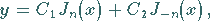 |
(9.53b) |
wobei 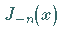 eine Reihe darstellt, die aus der Reihe für
eine Reihe darstellt, die aus der Reihe für 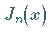 durch Ersetzen
von
durch Ersetzen
von  durch
durch 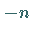 folgt.
Für ganzzahliges
folgt.
Für ganzzahliges  gilt
gilt 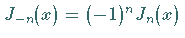 .
In der allgemeinen Lösung ist in diesem Falle
.
In der allgemeinen Lösung ist in diesem Falle 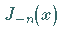 durch die
BESSELsche Funktion 2. Gattung
durch die
BESSELsche Funktion 2. Gattung
 |
(9.53c) |
auch WEBERsche Funktion genannt, zu ersetzen.
Zur Reihenentwicklung von 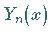 s. z.B. Lit. 9.26.
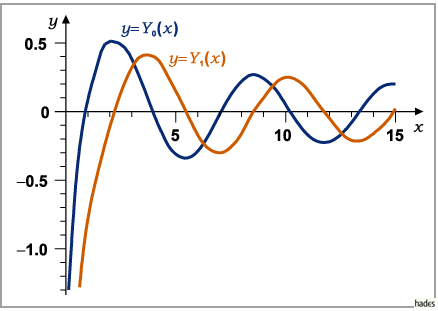
Die Kurvenbilder der Funktionen
s. z.B. Lit. 9.26.
Die Kurvenbilder der Funktionen 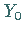 und
und 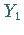 zeigt die folgende Abbildung.
zeigt die folgende Abbildung.
Bessel-Funktionen mit imaginären Variablen:
In manchen Anwendungen treten BESSEL-Funktionen mit einer rein imaginären
Variablen auf.
Dabei werden gewöhnlich die Produkte 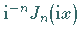 betrachtet, die mit
betrachtet, die mit
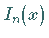 bezeichnet werden:
bezeichnet werden:
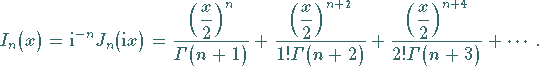 |
(9.54a) |
Hierbei handelt es sich um Lösungen der Differentialgleichung
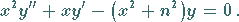 |
(9.54b) |
Eine zweite Lösung dieser Differentialgleichung ist die
MACDONALDsche Funktion
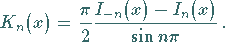 |
(9.54c) |
Wenn  gegen eine ganze Zahl konvergiert, strebt dieser Ausdruck einem Grenzwert zu.
gegen eine ganze Zahl konvergiert, strebt dieser Ausdruck einem Grenzwert zu.
Die Funktionen 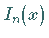 und
und 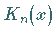 werden auch
modifizierte BESSEL- Funktionen genannt.
werden auch
modifizierte BESSEL- Funktionen genannt.
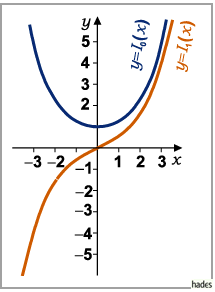
Die Kurvenbilder der Funktionen 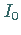 und
und 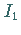 zeigt die folgende linke Abbildung,
die der Funktionen
zeigt die folgende linke Abbildung,
die der Funktionen 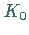 und
und 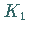 die rechte Abbildung.
die rechte Abbildung.
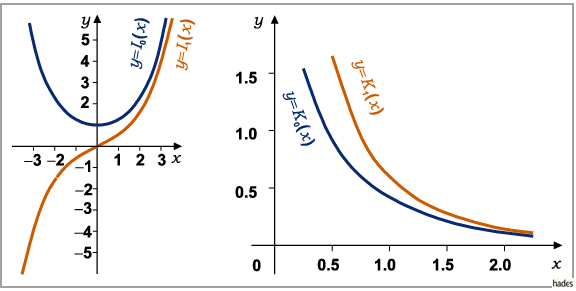
Werte der Funktionen
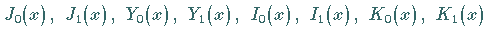 enthalten die Tabellen
BESSELsche Funktionen (Zylinderfunktionen).
enthalten die Tabellen
BESSELsche Funktionen (Zylinderfunktionen).
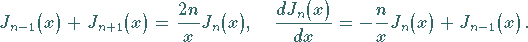 |
(9.55a) |
Die gleichen Formeln gelten auch für die WEBER-Funktionen 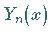
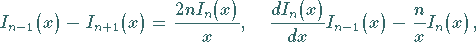 |
(9.55b) |
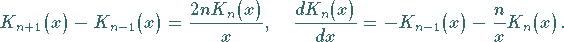 |
(9.55c) |
Für ganzzahliges  gilt
gilt
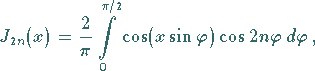 |
(9.55d) |
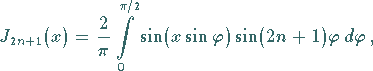 |
(9.55e) |
oder, in komplexer Form,
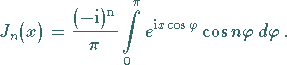 |
(9.55f) |
Die 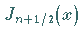 können durch elementare Funktionen ausgedrückt werden.
Insbesondere gilt
können durch elementare Funktionen ausgedrückt werden.
Insbesondere gilt
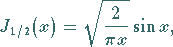 |
(9.56a) |
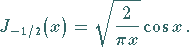 |
(9.56b) |
Durch sukzessive Anwendung der Rekursionsformeln (9.55a) bis
(9.55f) können die Ausdrücke für 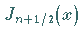 für
beliebige ganzzahlige
für
beliebige ganzzahlige  aufgeschrieben werden.
Für große Werte von
aufgeschrieben werden.
Für große Werte von 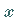 ergeben sich die folgenden asymptotischen Formeln:
ergeben sich die folgenden asymptotischen Formeln:
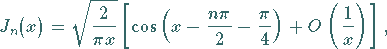 |
(9.57a) |
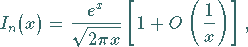 |
(9.57b) |
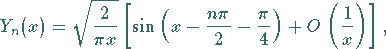 |
(9.57c) |
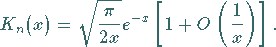 |
(9.57d) |
Der Ausdruck 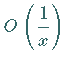 (s. LANDAU-Symbole)
bedeutet eine infinitesimale Größe der gleichen Ordnung wie
(s. LANDAU-Symbole)
bedeutet eine infinitesimale Größe der gleichen Ordnung wie 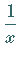 .
.
Weitere Angaben über BESSEL-Funktionen s. Lit. 21.1.
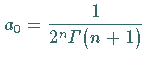 (
(![]() und
und ![]() werden auch
modifizierte BESSEL- Funktionen genannt.
werden auch
modifizierte BESSEL- Funktionen genannt.
![]() und
und ![]() zeigt die folgende linke Abbildung,
die der Funktionen
zeigt die folgende linke Abbildung,
die der Funktionen ![]() und
und ![]() die rechte Abbildung.
die rechte Abbildung.
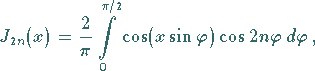
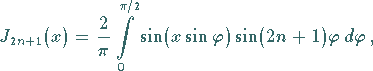
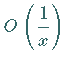 (s. LANDAU-Symbole)
bedeutet eine infinitesimale Größe der gleichen Ordnung wie
(s. LANDAU-Symbole)
bedeutet eine infinitesimale Größe der gleichen Ordnung wie