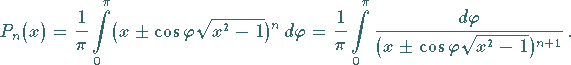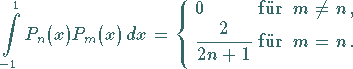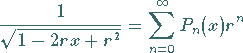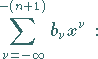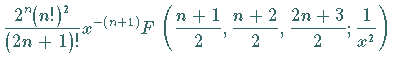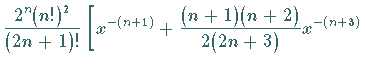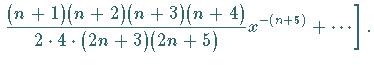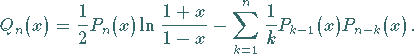Themen dieser Seite
Legendresche Differentialgleichung
Bei Beschränkung auf den Fall reeller Veränderlicher und ganzzahliger Parameter
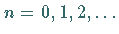 hat die LEGENDREsche Differentialgleichung die Gestalt
hat die LEGENDREsche Differentialgleichung die Gestalt
 |
(9.58a) |
Legendresche Polynome oder Kugelfunktionen 1. Art
LEGENDREsche Polynome oder Kugelfunktionen 1. Art heißen die partikulären
Lösungen der LEGENDREschen Differentialgleichung für ganzzahlige 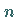 ,
die
sich über den Potenzreihenansatz
,
die
sich über den Potenzreihenansatz 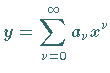 ermitteln
lassen:
ermitteln
lassen:
a) Definitionsgleichung:
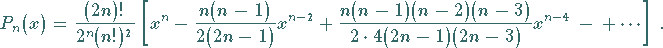 |
(9.58b) |
Dabei gilt 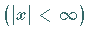 .
.
b) Andere Darstellung:
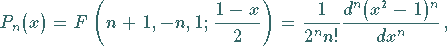 |
(9.58c) |
wobei mit 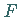 die hypergeometrische Reihe bezeichnet wird.
Die ersten acht Polynome haben die folgende einfache Form:
die hypergeometrische Reihe bezeichnet wird.
Die ersten acht Polynome haben die folgende einfache Form:
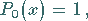 |
(9.58d) |
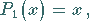 |
(9.58e) |
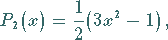 |
(9.58f) |
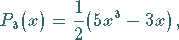 |
(9.58g) |
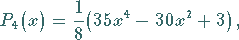 |
(9.58h) |
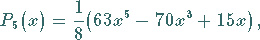 |
(9.58i) |
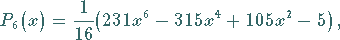 |
(9.58j) |
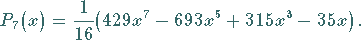 |
(9.58k) |
Die Kurvenbilder von  für Werte von
für Werte von  bis
bis  sind in der folgenden
Abbildung dargestellt.
sind in der folgenden
Abbildung dargestellt.
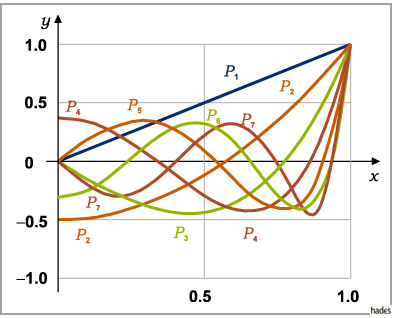
Zahlenwerte können leicht mit dem Taschenrechner berechnet bzw. in der
Tabelle ,, LEGENDREsche Polynome (Kugelfunktionen)``
nachgesehen werden.
Eigenschaften der Legendreschen Polynome 1. Art
a) Integraldarstellung:
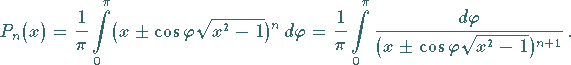 |
(9.59a) |
Das Vorzeichen kann in beiden Gleichungen beliebig genommen werden.
b) Rekursionsformel:
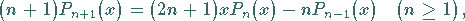 |
(9.59b) |
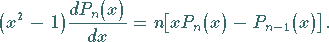 |
(9.59c) |
c) Orthogonalitätsrelation:
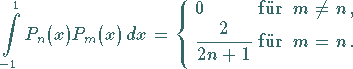 |
(9.59d) |
Zur Orthogonalität s. auch Orthogonale Systeme.
d) Nullstellensatz: Alle  Nullstellen von
Nullstellen von 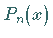 sind reell und einfach
und liegen im Intervall
sind reell und einfach
und liegen im Intervall 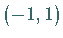 .
.
e) Erzeugende Funktion: Die LEGENDREschen Polynome 1. Art können auch
als Reihenentwicklung der Funktion
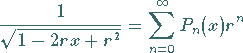 |
(9.59e) |
erzeugt werden.
Weitere Angaben über die LEGENDREschen Polynome 1. Art s. Lit. 21.1.
Eine zweite partikuläre, von 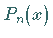 linear unabhängige Lösung
linear unabhängige Lösung 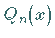 erhält
man für
erhält
man für 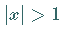 durch die Potenzreihenentwicklung
durch die Potenzreihenentwicklung
Die für 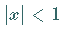 gültige Darstellung von
gültige Darstellung von 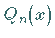 lautet:
lautet:
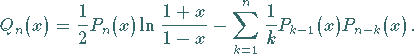 |
(9.60b) |
Man bezeichnet die Kugelfunktionen 1. und 2. Art auch als zugeordnete oder
assoziierte LEGENDREsche Funktionen
(s. auch Lösung der Polargleichung).
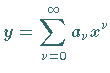 ermitteln
lassen:
ermitteln
lassen: