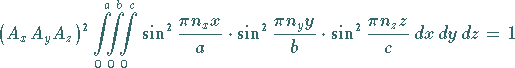Themen dieser Seite
Ein Teilchen mit der Masse 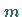 bewege sich kräftefrei in einem Quader mit
undurchlässigen Wänden der Kantenlänge
bewege sich kräftefrei in einem Quader mit
undurchlässigen Wänden der Kantenlänge 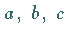 ,
so daß es sich
in einem Potentialkasten befindet, der in alle drei Raumrichtungen wegen seiner
Undurchlässigkeit unendlich hoch ist, d.h., die Aufenthaltswahrscheinlichkeit des
Teilchens und damit die Wellenfunktion
,
so daß es sich
in einem Potentialkasten befindet, der in alle drei Raumrichtungen wegen seiner
Undurchlässigkeit unendlich hoch ist, d.h., die Aufenthaltswahrscheinlichkeit des
Teilchens und damit die Wellenfunktion 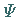 verschwinden außerhalb des Kastens.
Die SCHRÖDINGER-Gleichung und die Randbedingungen lauten für dieses Problem
verschwinden außerhalb des Kastens.
Die SCHRÖDINGER-Gleichung und die Randbedingungen lauten für dieses Problem
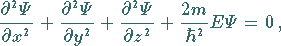 |
(9.113a) |
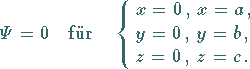 |
(9.113b) |
Mit dem Separationsansatz
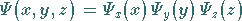 |
(9.114a) |
zur Variablentrennung ergibt sich nach Einsetzen in (9.113a)
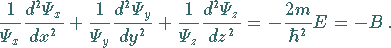 |
(9.114b) |
Jedes der drei Glieder auf der linken Seite hängt nur von einer unabhängigen
Variablen ab.
Ihre Summe kann für beliebige 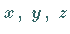 nur dann konstant gleich
nur dann konstant gleich 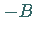 sein,
wenn jedes einzelne Glied für sich konstant ist.
In diesem Falle kann die partielle Differentialgleichung in drei gewöhnliche
Differentialgleichungen aufgespalten werden:
sein,
wenn jedes einzelne Glied für sich konstant ist.
In diesem Falle kann die partielle Differentialgleichung in drei gewöhnliche
Differentialgleichungen aufgespalten werden:
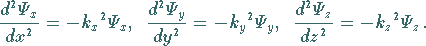 |
(9.114c) |
Zwischen den Separationskonstanten
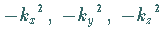 besteht der Zusammenhang
besteht der Zusammenhang
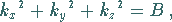 |
(9.114d) |
womit folgt
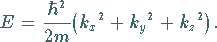 |
(9.114e) |
Lösungen
Lösungen der drei Gleichungen (9.114c) sind die Funktionen
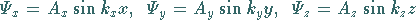 |
(9.115a) |
mit den Konstanten 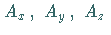 .
Damit erfüllt
.
Damit erfüllt 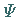 die Randbedingungen
die Randbedingungen
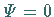 für
für 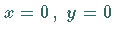 und
und  .
Um die Bedingung
.
Um die Bedingung 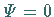 auch für
auch für 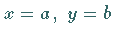 und
und
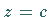 zu erfüllen, muß
zu erfüllen, muß
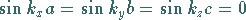 |
(9.115b) |
gelten, d.h., es müssen die Beziehungen
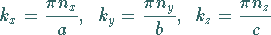 |
(9.115c) |
erfüllt sein, in denen 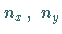 und
und 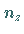 ganze Zahlen sind.
ganze Zahlen sind.
Für die Gesamtenergie erhält man damit
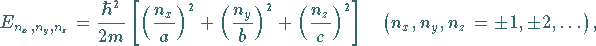 |
(9.115d) |
woraus folgt, daß Energieänderungen des Teilchens durch Austausch mit der
Umgebung nicht kontinuierlich, sondern lediglich in Quanten möglich sind.
Die Zahlen 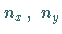 und
und 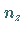 ,
die zu den Eigenwerten
der Energie gehören, werden Quantenzahlen genannt.
,
die zu den Eigenwerten
der Energie gehören, werden Quantenzahlen genannt.
Nach der Berechnung des Konstantenprodukts 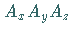 aus der
Normierungsbedingung
aus der
Normierungsbedingung
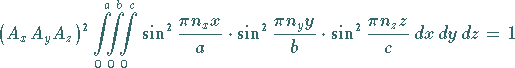 |
(9.115e) |
ergeben sich die vollständigen Eigenfunktionen des durch die drei
Quantenzahlen charakterisierten Zustandes zu
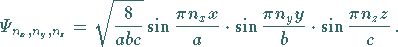 |
(9.115f) |
Die Eigenfunktionen verschwinden an den Wänden, weil eine der drei Sinusfunktionen
gleich Null ist.
Außer an den Wänden ist das immer dann der Fall, wenn die Beziehungen
erfüllt sind.
Somit gibt es 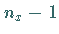 bzw.
bzw. 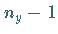 bzw.
bzw. 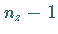 Ebenen senkrecht zur
Ebenen senkrecht zur 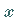 - bzw.
- bzw. 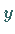 - bzw.
- bzw.
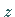 -Achse, in denen
-Achse, in denen 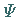 verschwindet.
Diese Ebenen heißen Knotenebenen .
verschwindet.
Diese Ebenen heißen Knotenebenen .
Spezialfall Würfel, Entartung
Im Spezialfalle des Würfels mit 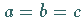 kann sich ein Teilchen gleichzeitig in
mehreren Zuständen befinden, die durch unterschiedliche linear unabhängige
Eigenfunktionen beschrieben werden und die gleiche Energie besitzen.
Das ist der Fall, wenn die Summe
kann sich ein Teilchen gleichzeitig in
mehreren Zuständen befinden, die durch unterschiedliche linear unabhängige
Eigenfunktionen beschrieben werden und die gleiche Energie besitzen.
Das ist der Fall, wenn die Summe 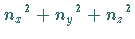 in verschiedenen
Zuständen den gleichen Wert hat.
Man spricht dann von entarteten Zuständen , und wenn es
in verschiedenen
Zuständen den gleichen Wert hat.
Man spricht dann von entarteten Zuständen , und wenn es 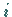 Zustände mit
gleicher Energie sind, von
Zustände mit
gleicher Energie sind, von 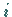 -facher Entartung .
-facher Entartung .
Die Quantenzahlen 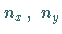 und
und 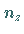 können alle ganzen Zahlen durchlaufen,
außer der Null.
Letzteres würde bedeuten, daß die Wellenfunktion identisch Null ist, d.h., das
Teilchen an keinem Ort innerhalb des Kastens existiert.
Somit muß die Teilchenenergie endlich bleiben, selbst wenn die Temperatur des
absoluten Nullpunktes erreicht ist.
Diese Nullpunktstranslationsenergie beträgt für den Quader
können alle ganzen Zahlen durchlaufen,
außer der Null.
Letzteres würde bedeuten, daß die Wellenfunktion identisch Null ist, d.h., das
Teilchen an keinem Ort innerhalb des Kastens existiert.
Somit muß die Teilchenenergie endlich bleiben, selbst wenn die Temperatur des
absoluten Nullpunktes erreicht ist.
Diese Nullpunktstranslationsenergie beträgt für den Quader
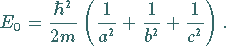 |
(9.115h) |
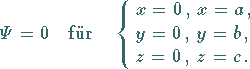
![]() .
Damit erfüllt
.
Damit erfüllt ![]() die Randbedingungen
die Randbedingungen
![]() für
für ![]() und
und ![]() .
Um die Bedingung
.
Um die Bedingung ![]() auch für
auch für ![]() und
und
![]() zu erfüllen, muß
zu erfüllen, muß