Themen dieser Seite
Begriff der Rauminversion:
Unter Koordinateninversion oder Rauminversion versteht man die
Spiegelung der Ortskoordinaten von Raumpunkten am Koordinatenursprung.
In einem dreidimensionalen kartesischen Koordinatensystem bedeutet Rauminversion
eine Umkehr der Vorzeichen der Koordinatenachsen:
 |
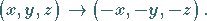(4.98) |
Dadurch wird ein rechtshändiges in ein linkshändiges Koordinatensystem überführt.
Analoges gilt für andere Koordinatensysteme.
In Kugelkoordinaten ergibt sich:
 |
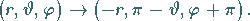(4.99) |
Bei Spiegelungen dieser Art bleiben die Längen von Vektoren und die Winkel zwischen
ihnen unverändert.
Der Übergang wird durch eine lineare Transformation vermittelt.
Die Transformationsmatrix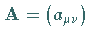 
einer linearen Transformation im
dreidimensionalen Raum gemäß (4.65) hat bei Rauminversion die folgenden
Eigenschaften:
 |
(4.100a) |
Für die Komponenten eines Tensors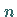 
-ter Stufe folgt damit aus (4.68)
 |
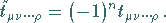(4.100b) |
Das bedeutet: Unter einer Punktspiegelung am Koordinatenursprung bleibt ein Tensor
0. Stufe, also ein Skalar, ungeändert, ein Tensor 1. Stufe, also ein Vektor, ändert
sein Vorzeichen, ein Tensor 2. Stufe bleibt ungeändert, usw.
