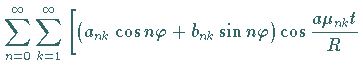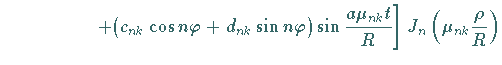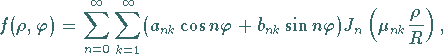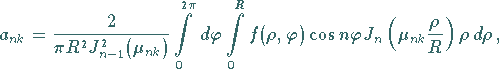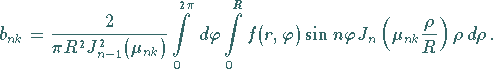Beschreibung der Schwingungen einer runden, am Rande eingespannten Membran.
Die Differentialgleichung ist linear, partiell und vom hyperbolischen Typ.
Sie hat in kartesischen Koordinaten bzw. in Polarkoordinaten die Form
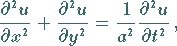 |
(9.92a) |
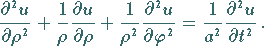 |
(9.92b) |
Die Anfangs- und Randbedingungen lauten
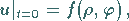 |
(9.92c) |
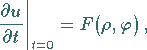 |
(9.92d) |
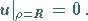 |
(9.92e) |
Zur Lösung wird die Methode der Variablentrennung
verwendet.
Einsetzen des Produktansatzes für die drei Variablen
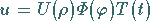 |
(9.92f) |
in die Differentialgleichung in Polarkoordinaten liefert
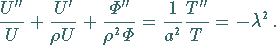 |
(9.92g) |
Daraus ergeben sich in Analogie zu den vorangegangenen Beispielen
Saitenschwingungsgleichung und
Stabschwingungsgleichung die folgenden Differentialgleichungen:
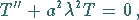 |
(9.92h) |
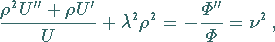 |
(9.92i) |
bzw.
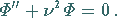 |
(9.92j) |
Aus den Bedingungen 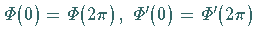 folgt
folgt
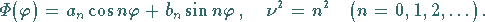 |
(9.92k) |
Aus 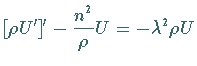 und
und 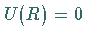 werden
werden 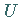 und
und
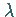 bestimmt.
Berücksichtigung der selbstverständlichen Bedingung der Beschränkung von
bestimmt.
Berücksichtigung der selbstverständlichen Bedingung der Beschränkung von 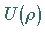 für
für 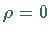 und Substitution von
und Substitution von 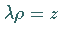 ergibt
ergibt
 |
(9.92l) |
wobei 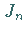 die BESSELschen Funktionen sind mit
die BESSELschen Funktionen sind mit
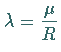 und
und 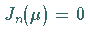 .
Das Funktionensystem
.
Das Funktionensystem
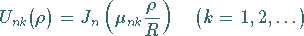 |
(9.92m) |
mit 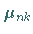 als
als 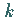 -te positive Nullstelle der Funktion
-te positive Nullstelle der Funktion 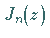 ist ein
vollständiges System aller Eigenfunktionen des selbstadjungierten Problems vom
STURM-LIOUVILLEschen Typ, die orthogonal mit dem
Gewicht
ist ein
vollständiges System aller Eigenfunktionen des selbstadjungierten Problems vom
STURM-LIOUVILLEschen Typ, die orthogonal mit dem
Gewicht 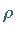 sind.
sind.
Die Lösung der Aufgabe wird in der Gestalt der Doppelreihe
angesetzt.
Aus den Anfangsbedingungen folgt für 
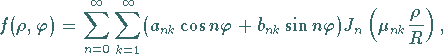 |
(9.92o) |
 |
(9.92p) |
woraus sich ergibt
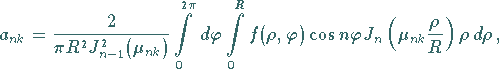 |
(9.92q) |
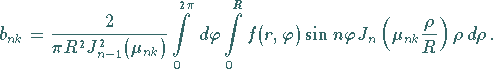 |
(9.92r) |
Im Falle  ist die im Zähler stehende
ist die im Zähler stehende 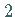 durch eine
durch eine 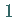 zu ersetzen.
Zur Bestimmung der Koeffizienten
zu ersetzen.
Zur Bestimmung der Koeffizienten 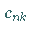 und
und 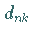 wird
wird 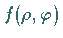 durch
durch 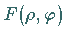 in den Formeln für
in den Formeln für 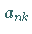 und
und 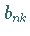 ersetzt
und mit
ersetzt
und mit 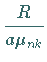 multipliziert.
multipliziert.
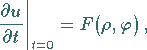
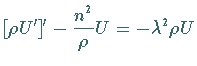 und
und 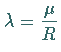 und
und