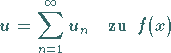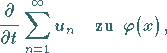Beispiel Saitenschwingungsgleichung
Saitenschwingungsgleichung wird die lineare partielle Differentialgleichung
2. Ordnung vom hyperbolischen Typ
 |
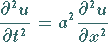(9.90a) |
genannt, mit deren Hilfe die Schwingungen einer gespannten Saite beschrieben werden.
Die Aufgabe besteht darin, diese Gleichung unter den Anfangs- und Randbedingungen
 |
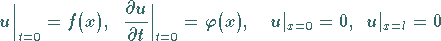(9.90b) |
zu lösen.
Zur Lösung wird die Methode der Variablentrennung
verwendet.
Mit einem Separationsansatz der Form
 |
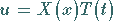(9.90c) |
liefert Einsetzen in die gegebene Differentialgleichung (9.90a)
die Gleichung
 |
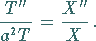(9.90d) |
Die Variablen sind getrennt, denn da die linke Seite nicht von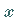 
und die rechte
nicht von 
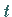abhängt, ist jede Seite für sich eine konstante Größe.
Die Konstante wird negativ gewählt und gleich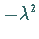 
gesetzt, da sich mit
nichtnegativen Werten nur die triviale Lösung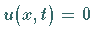 
ergibt.
Man erhält die zwei linearen Differentialgleichungen
 |
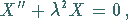(9.90e) |
 |
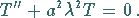(9.90f) |
Aus den Randbedingungen folgt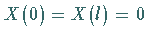 
.
Man sieht, daß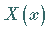 
eine Eigenfunktion des
STURM-LIOUVILLEschen Randwertproblems ist und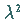 
der zugehörige Eigenwert.
Integration der Differentialgleichung (9.90e) für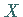 
und
Berücksichtigung der Randbedingungen ergibt
 |
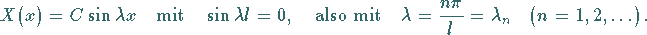(9.90g) |
Integration der Gleichung (9.90f) liefert für jeden Eigenwert
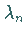jeweils eine partikuläre Lösung der ursprünglichen Differentialgleichung
(9.90a):
 |
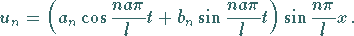(9.90h) |
Durch die Forderungen, daß für 
 |
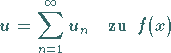(9.90i) |
wird und
 |
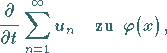(9.90j) |
ergibt sich mit Hilfe einer
FOURIER-Reihenentwicklung nach Sinusfunktionen
 |
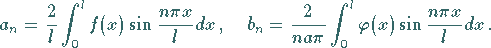(9.90k) |
