Sturm-Liouvillesches Problem
Für einen festen Wert des Parameters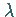 
gibt es zwei Fälle:
1. Das inhomogene Randwertproblem besitzt eine eindeutige Lösung bei beliebigem
,
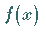während das zugehörige homogene Problem lediglich die triviale, identisch
verschwindende Lösung besitzt, oder
2. das zugehörige homogene Problem besitzt nichttriviale, d.h. nicht identisch
verschwindende Lösungen.
Dann ist das inhomogene Problem nicht für beliebige rechte Seiten lösbar; im
Falle der Existenz einer Lösung ist diese nicht eindeutig bestimmt.
Die Werte des Parameters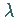 
,
für die der zweite Fall eintritt, d.h. das
homogene Problem eine nichttriviale Lösung hat, werden
Eigenwerte des Randwertproblems genannt, die zugehörigen nichttrivialen
Lösungen seine Eigenfunktionen .
Die Aufgabe, die Eigenwerte und Eigenfunktionen der Differentialgleichung
(9.64a) zu bestimmen, nennt man das
STURM- LIOUVILLEsche Problem .
