Beispiel Stabschwingungsgleichung
Stabschwingungsgleichung wird die lineare partielle Differentialgleichung 2. Ordnung
vom hyperbolischen Typ genannt, mit deren Hilfe die longitudinalen Schwingungen eines
Stabes beschrieben werden, dessen eines Ende frei ist und auf dessen zweites,
eingespanntes Ende im Anfangszeitpunkt eine konstante Kraft 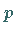 wirkt.
Zu lösen ist die gleiche Differentialgleichung wie im Beispiel
Saitenschwingungsgleichung, d.h.
wirkt.
Zu lösen ist die gleiche Differentialgleichung wie im Beispiel
Saitenschwingungsgleichung, d.h.
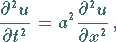 |
(9.91a) |
mit den gleichen Anfangs-, aber nunmehr inhomogenen Randbedingungen:
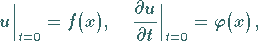 |
(9.91b) |
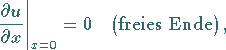 |
(9.91c) |
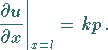 |
(9.91d) |
Diese Bedingungen können durch die homogenen Bedingungen
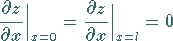 |
(9.91e) |
ersetzt werden, indem für 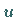 die neue unbekannte Funktion
die neue unbekannte Funktion
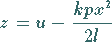 |
(9.91f) |
eingeführt wird.
Allerdings wird dann die Differentialgleichung inhomogen:
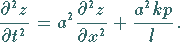 |
(9.91g) |
Zur Lösung wird die Methode der Variablentrennung
verwendet.
Die Lösung wird in Form der Summe 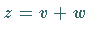 gesucht.
Dabei genügt
gesucht.
Dabei genügt 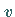 der homogenen Differentialgleichung sowie den Rand- und
Anfangsbedingungen für
der homogenen Differentialgleichung sowie den Rand- und
Anfangsbedingungen für 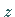 ,
d.h.
,
d.h.
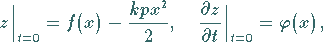 |
(9.91h) |
während 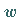 der inhomogenen Differentialgleichung genügt und die verschwindenden
Anfangs- und Randbedingungen erfüllt.
Daraus ergibt sich
der inhomogenen Differentialgleichung genügt und die verschwindenden
Anfangs- und Randbedingungen erfüllt.
Daraus ergibt sich 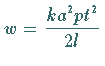 .
Eingehen in die Differentialgleichung mit dem Produktansatz
.
Eingehen in die Differentialgleichung mit dem Produktansatz
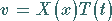 |
(9.91i) |
ergibt wie in Beispiel Saitenschwingungsgleichung für die
separierten Variablen:
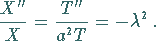 |
(9.91j) |
Integration der Differentialgleichung für 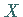 und Einsetzen der Randbedingungen
und Einsetzen der Randbedingungen
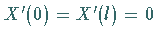 liefert die Eigenfunktionen
liefert die Eigenfunktionen
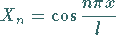 |
(9.91k) |
sowie die dazugehörigen Eigenwerte
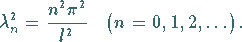 |
(9.91l) |
Durch das gleiche Vorgehen wie in Beispiel
Saitenschwingungsgleichung erhält man schließlich
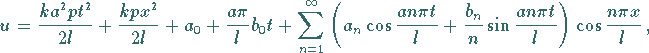 |
(9.91m) |
wobei 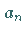 und
und 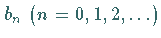 die Koeffizienten der
FOURIER-Reihenentwicklung für die Funktionen
die Koeffizienten der
FOURIER-Reihenentwicklung für die Funktionen
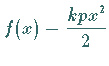 und
und 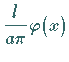 im Intervall
im Intervall
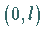 sind.
sind.
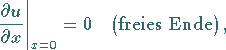
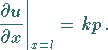
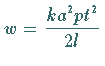 .
Eingehen in die Differentialgleichung mit dem Produktansatz
.
Eingehen in die Differentialgleichung mit dem Produktansatz
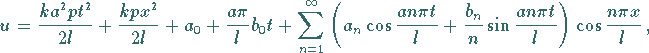
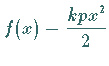 und
und 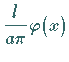 im Intervall
im Intervall