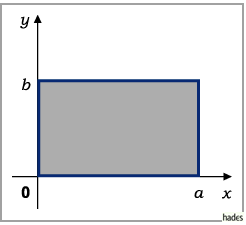
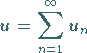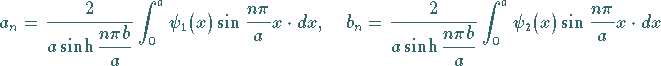für das Rechteck 
Zur Lösung wird die Methode der Variablentrennung
verwendet.
wird die Lösung der LAPLACEschen Differentialgleichung vom elliptischen Typ
 |
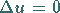(9.93a) |
mit Hilfe einer Funktion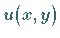 
gesucht, die auch die Randbedingungen
 |
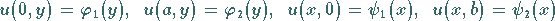(9.93b) |
erfüllt.
Als erster Schritt wird eine partikuläre Lösung für die Randbedingungen
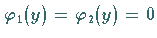bestimmt.
Einsetzen des Produktansatzes
 |
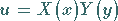(9.93c) |
in (9.93a) ergibt die Differentialgleichungen
 |
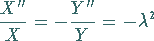(9.93d) |
mit dem Eigenwert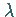 
in Analogie zu den oben betrachteten Aufgaben A bis
C.
Da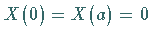 
gilt, ergibt sich
 |
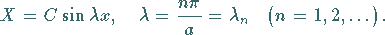(9.93e) |
Im zweiten Schritt wird die allgemeine Lösung der Differentialgleichung
 |
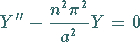(9.93f) |
in der Form
 |
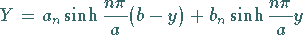(9.93g) |
hingeschrieben.
Daraus ergibt sich für die Randbedingungen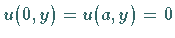 
eine partikuläre
Lösung von (9.93a) in der Form
 |
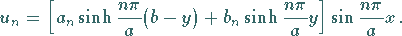(9.93h) |
Im dritten Schritt wird die allgemeine Lösung als Reihe
 |
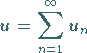(9.93i) |
angesetzt, so daß sich aus den Randbedingungen für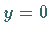 
und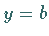 
 |
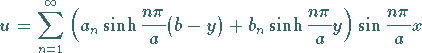(9.93j) |
mit den Koeffizienten
 |
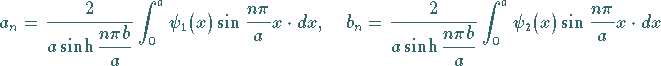(9.93k) |
ergibt.
In Analogie dazu wird die Aufgabe für die Randbedingungen
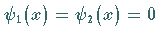gelöst, die in der Summe mit (9.93j)
die allgemeine Lösung von (9.93a) und
(9.93b) bildet.
