Vollständiges Differential
1. Definition:
Wenn 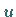 eine differenzierbare Funktion ist, wird die Summe (6.41b)
das vollständige Differential der Funktion genannt:
eine differenzierbare Funktion ist, wird die Summe (6.41b)
das vollständige Differential der Funktion genannt:
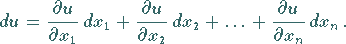 |
(6.42a) |
Mit Hilfe der Vektoren
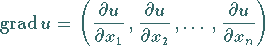 |
(6.42b) |
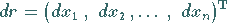 |
(6.42c) |
läßt sich das totale Differential als Skalarprodukt
 |
(6.42d) |
darstellen.
In der Gleichung (6.42b) handelt es sich um den Gradienten für
den Fall von 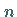 unabhängigen Variablen.
unabhängigen Variablen.
2. Haupteigenschaft des vollständigen Differentials wird in Analogie zum
Differential einer Funktion von einer Veränderlichen die in (6.38)
formulierte Invarianz in bezug auf die enthaltenen Variablen genannt.
3. Anwendung in der Fehlerrechnung:
Im Rahmen der Fehlerrechnung, z.B. bei der Betrachtung der
Fehlerfortpflanzung, wird das totale Differential 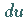 zur
Schätzung des Fehlers
zur
Schätzung des Fehlers 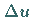 (s. (6.41a)) verwendet.
Aus der TAYLORschen Formel folgt
(s. (6.41a)) verwendet.
Aus der TAYLORschen Formel folgt
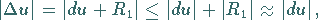 |
(6.43) |
d.h., der absolute Fehler  kann in erster Näherung durch
kann in erster Näherung durch 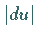 ersetzt
werden.
Damit ist
ersetzt
werden.
Damit ist 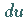 eine lineare Approximation für
eine lineare Approximation für 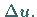
![]() kann in erster Näherung durch
kann in erster Näherung durch ![]() ersetzt
werden.
Damit ist
ersetzt
werden.
Damit ist ![]() eine lineare Approximation für
eine lineare Approximation für ![]()