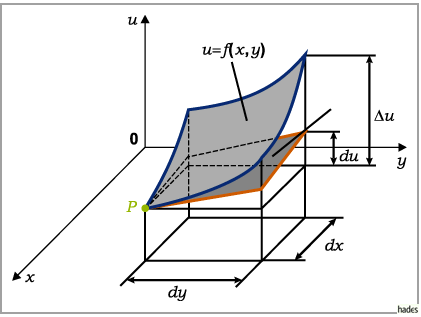
Geometrische Bedeutung des vollständigen Differentials
Die geometrische Bedeutung des vollständigen Differentials einer Funktion von zwei
Veränderlichen 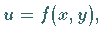 die in einem kartesischen Koordinatensystem als Fläche
dargestellt werden kann (obere Fläche durch den Punkt
die in einem kartesischen Koordinatensystem als Fläche
dargestellt werden kann (obere Fläche durch den Punkt 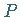 in der Abbildung), besteht
darin, daß
in der Abbildung), besteht
darin, daß 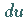 gleich dem Zuwachs der Applikate der
Tangentialebene (untere Fläche durch den betrachteten Punkt) ist, wenn
gleich dem Zuwachs der Applikate der
Tangentialebene (untere Fläche durch den betrachteten Punkt) ist, wenn 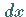 und
und 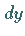 die Inkremente von
die Inkremente von 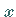 und
und 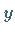 sind.
Mit
sind.
Mit 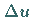 ist der Zuwachs der Applikate der Fläche für die Inkremente
ist der Zuwachs der Applikate der Fläche für die Inkremente 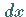 und
und
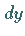 von
von 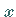 und
und 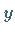 bezeichnet.
bezeichnet.
Aus der TAYLORschen Formel folgt für Funktionen von zwei
Variablen
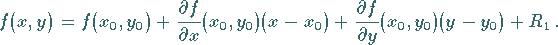 |
(6.44a) |
Vernachlässigt man das Restglied 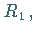 dann stellt
dann stellt
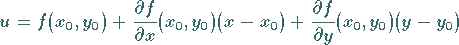 |
(6.44b) |
die Gleichung der Tangentialebene an die Fläche 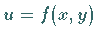 im Punkt
im Punkt
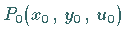 dar.
dar.