Begriff des vollständigen Differentials einer Funktion von mehreren Veränderlichen (totales Differential)
Differenzierbarkeit
Man nennt eine Funktion von mehreren Veränderlichen
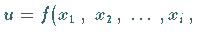
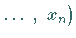im Punkt
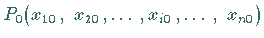differenzierbar, wenn sich der vollständige Zuwachs der Funktion
beim Übergang zu einem beliebig nahe benachbarten Punkt
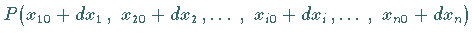mit den beliebig kleinen Größen
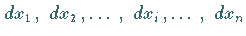von der Summe der
partiellen Differentiale der Funktion nach allen Variablen
 |
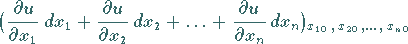(6.41b) |
um eine beliebig kleine Größe höherer Ordnung unterscheidet als der Abstand
 |
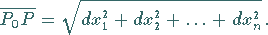(6.41c) |
Differenzierbar ist jede stetige Funktion von mehreren Variablen, die stetige partielle
Ableitungen nach allen ihren Variablen besitzt.
Umgekehrt folgt die Differenzierbarkeit einer Funktion nicht aus der bloßen Existenz
der partiellen Ableitungen.
