Haupteigenschaften des Differentials
1. Invarianz:
Unabhängig davon, ob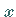 
eine unabhängige Variable oder eine Funktion von einer
weiteren Variablen 
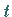ist, gilt
 |
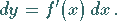(6.38) |
2. Größenordnung:
Wenn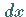 
eine beliebig kleine Größe ist, dann sind auch 
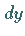und
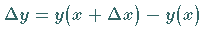beliebig kleine, aber äquivalente Größen, d.h.
.
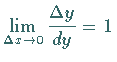Infolgedessen ist die Differenz zwischen ihnen ebenfalls eine beliebig kleine Größe,
aber von höherer Ordnung als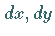 
und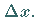 
Daraus ergibt sich die Beziehung
 |
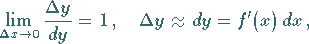(6.39) |
die es gestattet, die Berechnung kleiner Zuwächse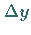 
( Inkremente )
auf die Berechnung ihres Differentials zurückzuführen.
Bei näherungsweisen Berechnungen, z.B. gemäß
Mittelwertsatz der Differentialrechnung oder mit
Fehlerfortpflanzungsgesetz wird davon Gebrauch gemacht.
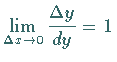