Mehrschrittverfahren
Das EULERsche Polygonzugverfahren (19.97) und das
RUNGE-KUTTA-Verfahren (19.99) stellen sogenannte
Einschrittverfahren dar, da sie bei der Berechnung von 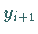 nur auf das
Ergebnis
nur auf das
Ergebnis 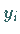 des vorangegangenen Schrittes zurückgreifen.
Allgemeine lineare Mehrschrittverfahren sind dagegen von der Form
des vorangegangenen Schrittes zurückgreifen.
Allgemeine lineare Mehrschrittverfahren sind dagegen von der Form
| |
|
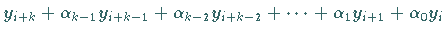 |
|
| |
|
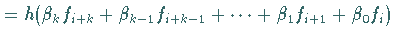 |
(19.101) |
mit geeignet gewählten Konstanten 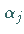 und
und
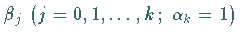 .
Die Vorschrift (19.101) wird als
.
Die Vorschrift (19.101) wird als 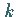 -Schrittverfahren bezeichnet, falls
-Schrittverfahren bezeichnet, falls
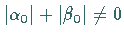 ist.
Es heißt explizit , falls
ist.
Es heißt explizit , falls 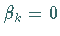 ist, weil dann in den Werten
ist, weil dann in den Werten
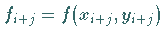 der rechten Seite von (19.101) nur die bereits
bekannten Näherungswerte
der rechten Seite von (19.101) nur die bereits
bekannten Näherungswerte  auftreten.
Ist
auftreten.
Ist 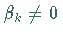 ,
so heißt das Verfahren implizit , da dann der gesuchte
neue Wert
,
so heißt das Verfahren implizit , da dann der gesuchte
neue Wert 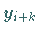 auf beiden Seiten von (19.101) auftritt.
Bei der Anwendung eines
auf beiden Seiten von (19.101) auftritt.
Bei der Anwendung eines 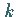 -Schrittverfahrens ist die Kenntnis von
-Schrittverfahrens ist die Kenntnis von 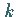 Startwerten
Startwerten
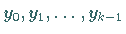 notwendig.
Diese verschafft man sich z.B. mit Hilfe eines Einschrittverfahrens.
notwendig.
Diese verschafft man sich z.B. mit Hilfe eines Einschrittverfahrens.
Spezielle Mehrschrittverfahren zur Lösung der Anfangswertaufgabe (19.93) kann
man dadurch gewinnen, daß man in (19.93) die Ableitung 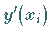 durch
Differenzenformeln ersetzt oder in (19.95) das Integral durch
Quadraturformeln approximiert.
durch
Differenzenformeln ersetzt oder in (19.95) das Integral durch
Quadraturformeln approximiert.
Beispiele für spezielle Mehrschrittverfahren sind:
1. Mittelpunktsregel: Die Ableitung 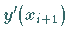 in (19.93)
wird durch die Sekantensteigung bezüglich der Stützstellen
in (19.93)
wird durch die Sekantensteigung bezüglich der Stützstellen 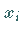 und
und 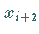 ersetzt.
Man erhält:
ersetzt.
Man erhält:
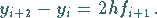 |
(19.102) |
2. Verfahren von Milne:
Das Integral in (19.95) wird durch die SIMPSON-Formel
approximiert.
Man erhält:
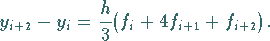 |
(19.103) |
3. Verfahren von Adams-Bashforth:Der Integrand in (19.95) wird durch das
Interpolationspolynom von LAGRANGE bezüglich der
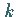 Stützstellen
Stützstellen
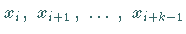 ersetzt.
Man integriert zwischen
ersetzt.
Man integriert zwischen 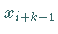 und
und 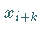 und erhält:
und erhält:
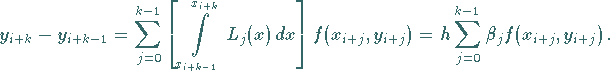 |
(19.104) |
Das Verfahren (19.104) ist explizit bezüglich 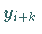 .
Zur Berechnung des Koeffizienten
.
Zur Berechnung des Koeffizienten 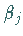 s. Lit. 19.1.
s. Lit. 19.1.
![]() durch
Differenzenformeln ersetzt oder in (19.95) das Integral durch
Quadraturformeln approximiert.
durch
Differenzenformeln ersetzt oder in (19.95) das Integral durch
Quadraturformeln approximiert.
![]() in (19.93)
wird durch die Sekantensteigung bezüglich der Stützstellen
in (19.93)
wird durch die Sekantensteigung bezüglich der Stützstellen ![]() und
und ![]() ersetzt.
Man erhält:
ersetzt.
Man erhält:
![]() Stützstellen
Stützstellen ![]() ersetzt.
Man integriert zwischen
ersetzt.
Man integriert zwischen ![]() und
und ![]() und erhält:
und erhält: