Hinweise
1. Für die spezielle Differentialgleichung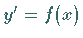 
geht das
RUNGE-KUTTA-Verfahren in die SIMPSON-Formel
über.
2. Bei einer sehr großen Anzahl von Integrationsschritten kann sich ein
Wechsel der Schrittweite als zweckmäßig oder sogar notwendig erweisen.
Über einen Schrittweitenwechsel kann mit Hilfe einer Fehlerschätzung entschieden
werden, die dadurch gewonnen wird, daß man die Rechnung etwa mit doppelter
Schrittweite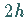 
wiederholt.
Hat man z.B. für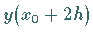 
die Näherungswerte 
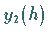(Rechnung mit einfacher
Schrittweite) und 
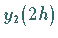(Rechnung mit doppelter Schrittweite) bestimmt, dann gilt
für den Fehler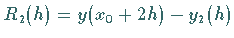 
die Schätzung
 |
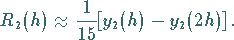(19.100) |
Informationen über die Realisierung der sogenannten Schrittweitensteuerung findet
man in der Literatur (s. Lit. 19.27).
3. RUNGE-KUTTA-Schemata für Differentialgleichungen höherer Ordnung
s. Lit. 19.27.
Andererseits können Differentialgleichungen höherer Ordnung in ein System von
Differentialgleichungen 1. Ordnung überführt werden
(s. Zurückführung auf ein System von Differentialgleichungen).
Dann besteht das Näherungsverfahren aus parallel durchgeführten Rechnungen gemäß
(19.99), die durch die Differentialgleichungen miteinander gekoppelt sind.
