Durch Integration erhält man aus der Anfangswertaufgabe zu (19.93) die
Integraldarstellung
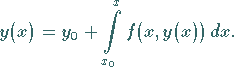 |
(19.95) |
Diese ist Ausgangspunkt für die Näherung
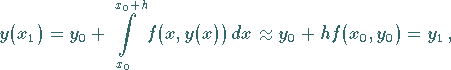 |
(19.96) |
die zu der folgenden Vorschrift des EULERschen Polygonzugverfahrens
verallgemeinert wird:
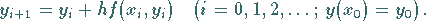 |
(19.97) |
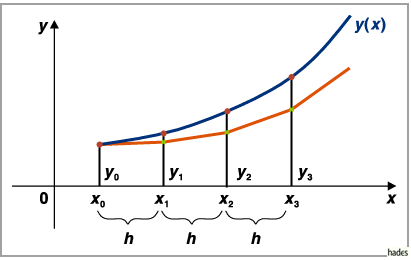
Zur geometrischen Interpretation (s. Abbildung).
Vergleicht man (19.96) mit der TAYLORentwicklung
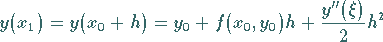 |
(19.98) |
mit 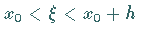 ,
dann sieht man, daß die Näherung
,
dann sieht man, daß die Näherung 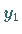 für den
exakten Wert
für den
exakten Wert 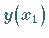 einen Fehler von der Größenordnung
einen Fehler von der Größenordnung 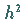 hat.
Die Genauigkeit kann durch Verkleinerung der Schrittweite
hat.
Die Genauigkeit kann durch Verkleinerung der Schrittweite 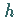 erhöht werden.
Praktische Rechnungen zeigen, daß sich bei Halbierung der Schrittweite
erhöht werden.
Praktische Rechnungen zeigen, daß sich bei Halbierung der Schrittweite 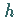 auch der
Fehler der Näherungen
auch der
Fehler der Näherungen 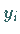 etwa halbiert.
etwa halbiert.
Mit Hilfe des EULERschen Polygonzugverfahrens kann man sich sehr schnell einen
Überblick über den ungefähren Verlauf der Lösungskurve verschaffen.
![]() ,
dann sieht man, daß die Näherung
,
dann sieht man, daß die Näherung ![]() für den
exakten Wert
für den
exakten Wert ![]() einen Fehler von der Größenordnung
einen Fehler von der Größenordnung ![]() hat.
Die Genauigkeit kann durch Verkleinerung der Schrittweite
hat.
Die Genauigkeit kann durch Verkleinerung der Schrittweite ![]() erhöht werden.
Praktische Rechnungen zeigen, daß sich bei Halbierung der Schrittweite
erhöht werden.
Praktische Rechnungen zeigen, daß sich bei Halbierung der Schrittweite ![]() auch der
Fehler der Näherungen
auch der
Fehler der Näherungen ![]() etwa halbiert.
etwa halbiert.