Hypergeometrische Differentialgleichung
Hypergeometrische Differentialgleichung heißt die Gleichung
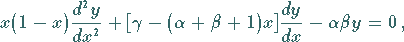 |
(9.61a) |
in der die 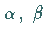 und
und 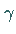 Parameter sind.
Sie beinhaltet eine große Zahl wichtiger Spezialfälle.
Parameter sind.
Sie beinhaltet eine große Zahl wichtiger Spezialfälle.
a) Für 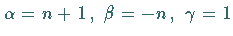 und
und 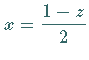 ergibt sich die LEGENDREsche Differentialgleichung.
ergibt sich die LEGENDREsche Differentialgleichung.
b) Für 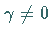 oder
oder 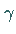 keine ganze negative Zahl ergibt sich
als partikuläre Lösung die hypergeometrische Reihe oder
hypergeometrische Funktion :
keine ganze negative Zahl ergibt sich
als partikuläre Lösung die hypergeometrische Reihe oder
hypergeometrische Funktion :
die für 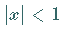 absolut konvergiert.
Die Konvergenz der hypergeometrischen Reihe hängt für
absolut konvergiert.
Die Konvergenz der hypergeometrischen Reihe hängt für 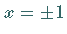 von der Zahl
von der Zahl
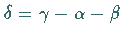 ab.
Für
ab.
Für 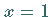 konvergiert sie, falls
konvergiert sie, falls 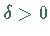 ist, für
ist, für 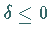 divergiert
sie.
Für
divergiert
sie.
Für 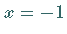 ergibt
ergibt 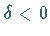 absolute Konvergenz,
absolute Konvergenz, 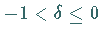 bedingte
Konvergenz und
bedingte
Konvergenz und 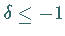 Divergenz.
Divergenz.
c) Für 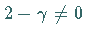 oder ungleich einer ganzen negativen Zahl ergibt sich
als partikuläre Lösung die Funktion
oder ungleich einer ganzen negativen Zahl ergibt sich
als partikuläre Lösung die Funktion
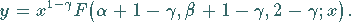 |
(9.61c) |
d) In einigen Fällen wird die hypergeometrische Reihe zu einer elementaren
Funktion, z.B.:
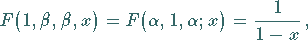 |
(9.61d) |
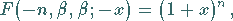 |
(9.61e) |
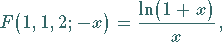 |
(9.61f) |
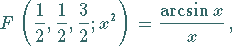 |
(9.61g) |
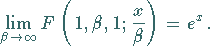 |
(9.61h) |
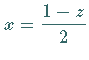 ergibt sich die LEGENDREsche Differentialgleichung.
ergibt sich die LEGENDREsche Differentialgleichung.