|
|
|
|
| (9.43a) |
| (9.43b) |
| (9.43c) |
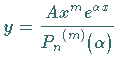 eine partikuläre Lösung.
Diese Formeln können durch Anwendung des Zerlegungssatzes auch verwendet werden, wenn
eine partikuläre Lösung.
Diese Formeln können durch Anwendung des Zerlegungssatzes auch verwendet werden, wenn
| (9.43d) |
| (9.43e) |
| Beispiel A | |
|
Für die Differentialgleichung | |
| Beispiel B | |
|
Die Differentialgleichung | |
Eine partikuläre Lösung kann immer in der gleichen Form gefunden werden, d.h. als
Ausdruck ![]() .
.
![]() ist ein mit
ist ein mit ![]() multipliziertes Polynom
multipliziertes Polynom ![]() -ten Grades, wenn
-ten Grades, wenn ![]() eine
eine
![]() -fache Wurzel der charakteristischen Gleichung ist.
Geht man von einem Lösungsansatz mit unbestimmten Koeffizienten des Polynoms
-fache Wurzel der charakteristischen Gleichung ist.
Geht man von einem Lösungsansatz mit unbestimmten Koeffizienten des Polynoms ![]() aus und fordert man, daß er der gegebenen inhomogenen Differentialgleichung genügt,
dann können die unbekannten Koeffizienten aus einem Satz linearer algebraischer
Gleichungen bestimmt werden.
Die Methode ist besonders in den Fällen
aus und fordert man, daß er der gegebenen inhomogenen Differentialgleichung genügt,
dann können die unbekannten Koeffizienten aus einem Satz linearer algebraischer
Gleichungen bestimmt werden.
Die Methode ist besonders in den Fällen ![]() für
für ![]() und
und
![]() oder
oder ![]() für
für ![]() anwendbar.
Hier wird eine Lösung der Form
anwendbar.
Hier wird eine Lösung der Form
![]() gesucht.
gesucht.
| Beispiel | |
|
Die Wurzeln der zur Differentialgleichung | |
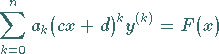 |
(9.44a) |
| (9.44b) |
| Beispiel | |
|
Die Differentialgleichung | |
|
|
|