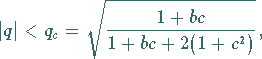Auftreten
Raum-zeitliche Variationen nichtlinearer Wellen
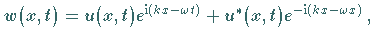die auf der Längenskala 
und der Zeitskala 
klein sind,
können durch orts- und zeitabhängige Einhüllende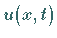 
beschrieben werden.
Soche Wellen treten in dissipativen Systemen auf, z.B. in der Hydrodynamik oder
bei chemischen Reaktionen.
Gleichung und Lösungen
Die GGL-Gleichung für das komplexe Fels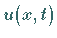
lautet
 |
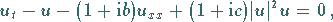(9.159) |
wobei die beiden komplexen Parameter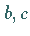 
systemspezifisch sind.
Die Gleichung (9.159) ist ein Beispiel für eine nichtlineare dissipative
Evolutionsgleichung.
1.
Für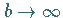 
und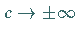 
geht (9.159)
nach einer geeigneten Transformation in die NLS-Gleichung (9.139) über.
2.
Der Spezialfall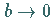 
und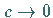 
( GINSBURG-LANDAU-(GL)-Gleichung) ist eine wichtige Gleichung der statistischen
Physik des thermodynamischen Gleichgewichtes und irreversibler Prozesse.
Sie beschreibt die Supraleitung in der Nähe des Phasenüberganges Supra-Normalleitung.
In dissipativen strukturbildenden Prozessen, wie z.B. der
RAYLEIGH-BENARD-Konvektion
beschreibt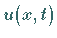
die Einhüllende einer stationären, räumlich periodischen Struktur
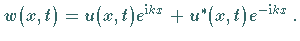Lösungen einfacher Art sind ebene Wellen:
 |
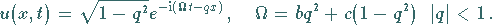(9.160) |
Lösungen existieren für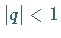 
und sinmd stabil gegenüber
schwachen langwelligen Störungen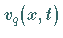 
in einem Wellenband
 |
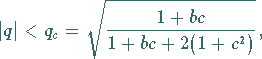(9.161) |
wobei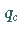 
die ECKHAUS-Wellenzahl ist.
Für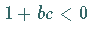 
( NEWELL-Kriterium) sind keine der Wellen
(9.160) stabil ( BENJAMIN-FEIR-Instabilität) und
die Lösungen von (9.159) sind raum-zeitlich
ungeordnet; man spricht dann auch vom raum-zeitlichen Chaos.
In zwei Raumdimensionen besitzt (9.159) mit der Ersetzung
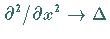Spirallösungen, wie sie z.B. bei chemischen
Reaktionen zu beobachten sind.
Auf Grund der Nichtlinearität sind lineare Superpositionen der Wellen (9.160)
keine Lösungen von (9.159).
