Die NLS-Gleichung für die Evolutionsfunktion 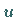 und ihre Solitonlösung lauten:
und ihre Solitonlösung lauten:
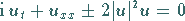 |
(9.139) |
und
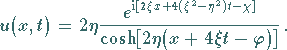 |
(9.140) |
Hier ist 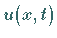 komplex.
Das NLS-Soliton ist durch
komplex.
Das NLS-Soliton ist durch 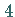 dimensionslosen Parameter
dimensionslosen Parameter 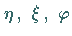 und
und 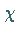 charakterisiert.
Die Einhüllende des Wellenpakets bewegt sich mit der Geschwindigkeit
charakterisiert.
Die Einhüllende des Wellenpakets bewegt sich mit der Geschwindigkeit 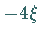 ,
die
Phasengeschwindigkeit der eingehüllten Welle ist
,
die
Phasengeschwindigkeit der eingehüllten Welle ist 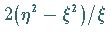 .
.
Im Unterschied zum KdV-Soliton (9.135) können hier die Amplitude
(über 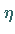 )
und die Geschwindigkeit (über
)
und die Geschwindigkeit (über 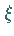 )
unabhängig voneinander gewählt
werden.
)
unabhängig voneinander gewählt
werden.
Im Falle von 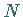 wechselwirkenden Solitonen werden diese durch
wechselwirkenden Solitonen werden diese durch 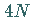 willkürlich
wählbare Parameter charakterisiert:
willkürlich
wählbare Parameter charakterisiert:
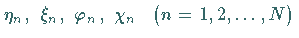 .
Falls die Solitonen verschiedene Geschwindigkeiten haben, zerfällt die
.
Falls die Solitonen verschiedene Geschwindigkeiten haben, zerfällt die
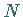 -Solitonenlösung asymptotisch für
-Solitonenlösung asymptotisch für 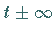 in eine Summe von
in eine Summe von 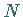 individuellen Solitonen der Form (9.140).
individuellen Solitonen der Form (9.140).
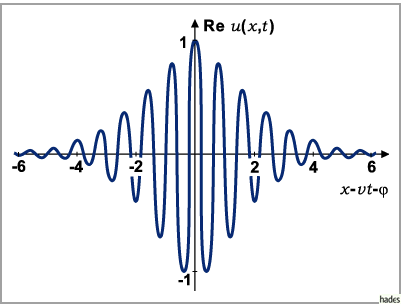
Die Abbildung zeigt eine Darstellung des Realteiles von (9.140) mit
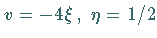 und
und 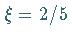 .
.