Periodische Muster und nichtlineare Wellen
Solche nichtlinearen Erscheinungen treten in einer Reihe von klassischen dissipativen
(d.h. Reibung oder Dämpfung enthaltenden) Systemen auf, wenn eine äußere Kraft
hinreichend groß ist.
Befindet sich z.B. eine Flüssigkeitsschicht im Gravitationsfeld,
und wird sie von unten erwärmt, so entspricht die Temperaturdifferenz zwischen ihrem
unterem und oberem Rand einer äußeren Kraft.
Durch die Erwärmung steigt die untere Schicht, so daß die Schichtung instabil
wird.
Bei hinreichend großer Temperaturdifferenz geht die instabile Schichtung spontan
in periodisch angeordnete Konvektionszellen über.
Man spricht von Gabelverzweigung oder Bifurkation aus dem nur
wärmeleitenden Zustand (ohne Konvektion) in die wohlgeordnete
RAYLEIGH-BENARD-Konvektion.
Eine Wegnahme der äußeren Kraft führt infolge der Dissipation zum Abklingen der
Wellen (hier der zellularen Konvektion).
Eine Verstärkung der äußeren Kraft stört die geordnete Konvektion bis hin
zur turbulenten Konvektion (Chaos).
Auch bei chemischen Reaktionen können derartige Phänomene auftreten.
Wichtige Beispiele für Gleichungen solcher Phänomene sind:
a)
GINSBURG-LANDAU-(GGL)-Gleichung, generalisiert von STUART und NEWELL
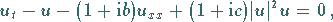 |
(9.132) |
b) KURAMOTO-SIVASHINSKY-(KS)-Gleichung
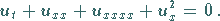 |
(9.133) |
Im Unterschied zu den oben genannten Gleichungen (KdV, NLS, SG), die keine Dissipation
enthalten, handelt es sich bei der GGL- und der KS-Gleichung um nichtlineare
dissipative Gleichungen.
Neben raum-zeitlich periodischen Lösungen (nichtlineare Wellen) haben sie auch
raum-zeitlich ungeordnete (chaotische) Lösungen.
Charaklteristisch ist das Auftreten raum-zeitlicher Muster oder Strukturen
einschließlich des Überganges zum Chaos.