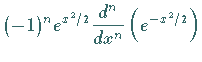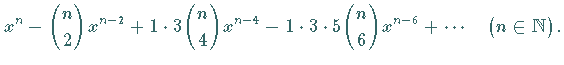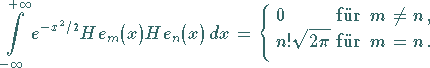Hermitesche Differentialgleichung
In der Literatur sind zwei Definitionsgleichungen der HERMITEschen
Differentialgleichung gebräuchlich:
Definitionsgleichung zu Variante 1:
 |
(9.63a) |
Definitionsgleichung zu Variante 2:
 |
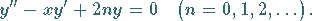(9.63b) |
Partikuläre Lösungen sind die HERMITEschen Polynome , die entsprechend in
zwei Varianten auftreten, als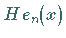 
zu Definitionsgleichung 1 und als 
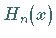zu
Definitionsgleichung 2.
HERMITEschen Polynome zu Definitionsgleichung 1:
Für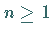 
gelten die folgenden Rekursionsformeln:
 |
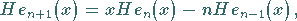(9.63d) |
 |
(9.63e) |
Die Orthogonalitätsrelation lautet:
 |
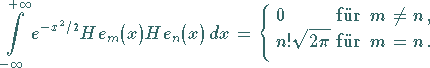(9.63f) |
Hermitesche Polynome zu Definitionsgleichung 2:
 |
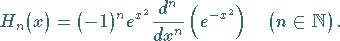(9.63g) |
Bezüglich der ersten Polynome s. Physikalische Lösungen.
Der Zusammenhang mit den HERMITEschen Polynomen zur 1. Definitionsgleichung lautet:
 |
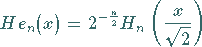(9.63h) |
Zur Orthogonalität s. auch Orthogonale Systeme.
