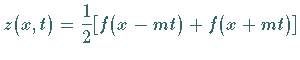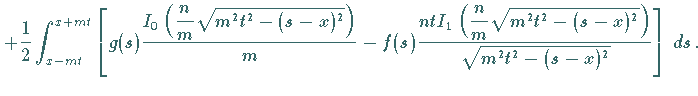Beispiel Telegraphengleichung
Telegraphengleichung nennt man die lineare partielle Differentialgleichung 2. Ordnung
vom hyperbolischen Typ
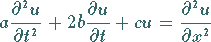 |
(9.96a) |
mit den Konstanten 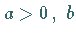 und
und 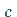 ,
die das Fließen des elektrischen
Stromes in Leitungen beschreibt.
Sie stellt eine Verallgemeinerung der Saitenschwingungsgleichung
dar.
,
die das Fließen des elektrischen
Stromes in Leitungen beschreibt.
Sie stellt eine Verallgemeinerung der Saitenschwingungsgleichung
dar.
Die unbekannte Funktion 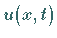 wird durch die Substitution
wird durch die Substitution 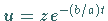 ersetzt, so daß (9.96a) übergeht in
ersetzt, so daß (9.96a) übergeht in
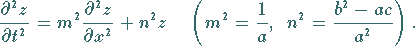 |
(9.96b) |
Durch die Substitutionen der unabhängigen Variablen
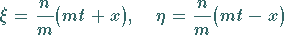 |
(9.96c) |
erhält man schließlich die Normalform
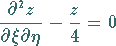 |
(9.96d) |
der linearen partiellen Differentialgleichung vom hyperbolischen Typ.
Dieser Differentialgleichung muß die RIEMANNsche Funktion
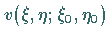 genügen und für
genügen und für 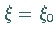 sowie
sowie 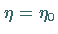 den Wert Eins annehmen.
Wenn in
den Wert Eins annehmen.
Wenn in 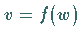 für
für 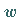 die Gestalt
die Gestalt
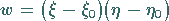 |
(9.96e) |
gewählt wird, dann ist 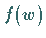 eine Lösung der Differentialgleichung
eine Lösung der Differentialgleichung
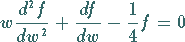 |
(9.96f) |
mit der Anfangsbedingung 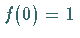 .
Die Substitution
.
Die Substitution 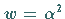 überführt diese Differentialgleichung in die
BESSELsche Differentialgleichung nullter Ordnung
überführt diese Differentialgleichung in die
BESSELsche Differentialgleichung nullter Ordnung
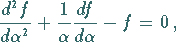 |
(9.96g) |
so daß die Lösung lautet
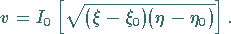 |
(9.96h) |
Eine Lösung der ursprünglichen Differentialgleichung (9.96a) mit den
Anfangsbedingungen
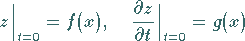 |
(9.96i) |
kann erhalten werden, indem man den gefundenen Wert von 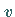 in die RIEMANNsche
Formel einsetzt und zu den ursprünglichen Variablen zurückkehrt:
in die RIEMANNsche
Formel einsetzt und zu den ursprünglichen Variablen zurückkehrt:
| |
|
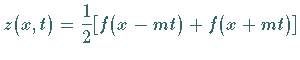 |
|
| |
|
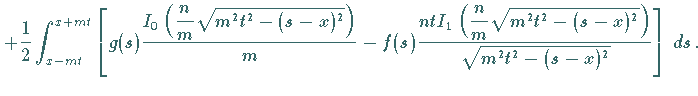 |
(9.96j) |