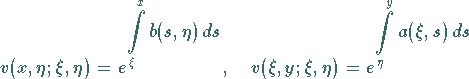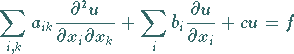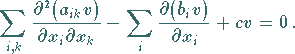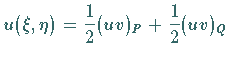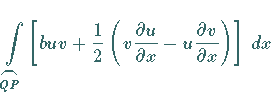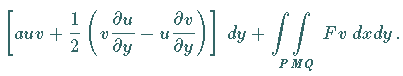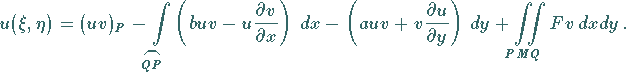Riemannsche Methode zur Lösung des Cauchyschen Problems der hyperbolischen Differentialgleichung
 |
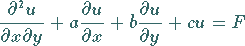(9.95a) |
1. Riemannsche Funktion
heißt die Funktion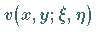 
,
wobei 
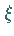und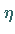 
als Parameter
aufgefaßt werden, die der zu (9.95a) konjugierten homogenen
Differentialgleichung
 |
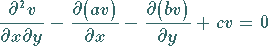(9.95b) |
und den Bedingungen
 |
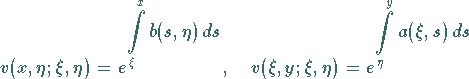(9.95c) |
genügt.
Allgemein haben lineare Differentialgleichungen 2. Ordnung und die zu ihnen
konjugierten Differentialgleichungen die folgende Form:
 |
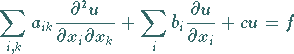(9.95d) |
und
 |
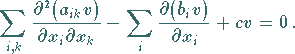(9.95e) |
2. Riemannsche Formel
wird die Integralformel genannt, mit deren Hilfe die Funktion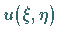 
bestimmt wird, die der gegebenen Differentialgleichung (9.95a)
genügt und die auf einer vorgegebenen Kurve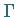 
(s. Abbildung)
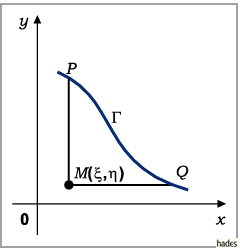
zusammen mit ihrer Ableitung nach der Richtung der Kurvennormalen
vorgegebene Werte annimmt:
Die glatte Kurve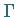
darf keine zu den Koordinatenachsen parallelen Tangenten
besitzen, d.h., sie darf die Charakteristiken nicht berühren.
Das Kurvenintegral in dieser Formel kann berechnet werden, da aus den Werten der Funktion
und ihrer Ableitung nach einer nichttangentialen Richtung längs des Kurvenbogens die
Werte beider partieller Ableitungen ermittelbar sind.
Oft werden beim CAUCHYschen Problem anstelle der Normalenableitung auf der Kurve die
Werte einer partiellen Ableitung der gesuchten Funktion vorgegeben, z.B.
.
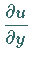Dann wird eine andere Form der RIEMANNschen Formel verwendet:
 |
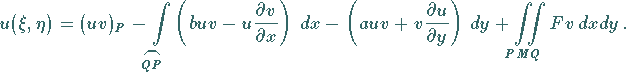(9.95g) |
