Singulärer Punkt

Themen dieser Seite

Singulärer Punkt

Singulärer Punkt ist der allgemeine Begriff für verschiedene spezielle Kurvenpunkte.

Arten singulärer Punkte

Die angegebenen singulären Punkte sind in den danach folgenden Abbildungen dargestellt.

a) Doppelpunkte: In Doppelpunkten schneidet sich die Kurve selbst (linke obere Abbildung).
b) Isolierte Punkte: Die isolierten Punkte genügen der Kurvengleichung; sie befinden sich aber außerhalb der Kurve (mittlere obere Abbildung).
c), d) Rückkehrpunkte: In Rückkehrpunkten ändert sich der Durchlaufsinn; man unterscheidet je nach der Lage der Tangente zu den Kurvenzweigen Rückkehrpunkte 1. und 2. Art (dritte obere und erste untere Abbildung).
e) Selbstberührungspunkte: In Selbstberührungspunkten berührt sich die Kurve selbst (rechte untere Abbildung).

f) Knickpunkte: In Knickpunkten ändert die Kurve sprunghaft ihre Richtung, aber im Unterschied zum Rückkehrpunkt gibt es zwei verschiedene Tangenten für die zwei Kurvenzweige (obere linke Abbildung).
g) Abbrechpunkte: In Abbrechpunkten bricht die Kurve ab (mittlere obere Abbildung).
h) Asymptotische Punkte: Um asymptotische Punkte windet sich die Kurve unendliche Male herum, wobei sie sich ihm beliebig nähert (obere rechte Abbildung).
i), k) Mehrere Singularitäten: Es können auch zwei oder drei derartige Singularitäten in einem Punkt auftreten (zwei untere Abbildungen).

Bestimmung von Selbstberührungs-, Knick- und Abbrechpunkten

Singularitäten dieser Art treten nur bei Kurven transzendenter Funktionen auf.
Den Knickpunkten entspricht ein endlicher Sprung der Ableitung

Punkten, in denen die Kurve abbricht, entsprechen Unstetigkeitsstellen der Funktion

mit endlichem Sprung oder ein direkter Abbruch.
Asymptotische Punkte lassen sich am einfachsten für Kurven bestimmen, die in Polarkoordinaten gemäß

gegeben sind. Wenn für

oder

der Grenzwert

wird, ist der Pol ein asymptotischer Punkt.

Beispiel A

Der Koordinatenursprung ist für die Kurve ein Knickpunkt.

Beispiel B

Die Punkte (1,0) und (1,1) der Funktion sind Unstetigkeitsstellen.

Beispiel C

Die logarithmische Spirale besitzt einen asymptotischen Punkt.

Bestimmung von Mehrfachpunkten (Fälle a) bis e) sowie i) und j))

Doppelpunkte, Dreifachpunkte usw. werden unter der Bezeichnung Mehrfachpunkte zusammengefaßt. Zu ihrer Bestimmung wird die Kurve ausgehend von der Gleichungsform

untersucht. Ein Punkt

mit den Koordinaten

die gleichzeitig die drei Gleichungen

und

erfüllen, ist ein Doppelpunkt, wenn von den drei Ableitungen 2. Ordnung

und

wenigstens eine nicht verschwindet. Im entgegengesetzten Falle ist

ein Dreifachpunkt oder ein Punkt mit höherer Mehrfachheit.
Die Eigenschaften eines Doppelpunktes hängen vom Vorzeichen der Funktionaldeterminante ab:

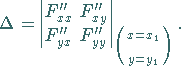(3.475)

1. : Für schneidet sich die Kurve selbst im Punkt die Richtungskoeffizienten der Tangenten in ergeben sich als Wurzeln der Gleichung

(3.476)

2. : Für ist ein isolierter Punkt.
3. : Für ist entweder ein Rückkehr- oder ein Selbstberührungspunkt; der Richtungskoeffizient der Tangente ist

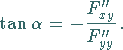(3.477)

Zur genaueren Untersuchung des Mehrfachpunktes empfiehlt es sich, das Koordinatensystem in den Punkt zu verlegen und so zu drehen, daß die -Achse zur Kurventangente im Punkt wird. Aus der Gestalt der Gleichung kann dann erkannt werden, ob es sich um einen Rückkehrpunkt 1. oder 2. Art handelt oder um einen Selbstberührungspunkt.

Beispiel A

Untersuchung der Lemniskate mit

Das Gleichungssystem liefert die drei Lösungen von denen nur die erste der Bedingung genügt. Einsetzen von (0,0) in die 2. Ableitungen ergibt d.h., im Koordinatenursprung schneidet sich die Kurve selbst; die Richtungskoeffizienten der Tangenten ergeben sich zu ihre Gleichungen lauten

Beispiel B

von den Punkten (0,0), und liegt nur der erste auf der Kurve. Weiter ist d.h., der Koordinatenursprung ist ein isolierter Punkt.

Beispiel C

Die Gleichungen liefern nur die eine Lösung (0,0), die auch die Gleichung erfüllt. Außerdem ist und so daß der Koordinatenursprung ein Rückkehrpunkt 2. Art ist, was auch aus der expliziten Form der Gleichung erkannt werden kann. Für ist nicht definiert, während für beide -Werte positiv sind; im Koordinatenursprung verläuft die Tangente horizontal.

Algebraische Kurven, gegeben als Polynom in x und y

Wenn die Gleichung keine konstanten Glieder und keine Glieder ersten Grades enthält, dann ist der Koordinatenursprung ein Doppelpunkt. Die Gleichung zur Bestimmung der zugehörigen Tangenten erhält man durch Nullsetzen der Summe der Glieder 2. Grades. Wenn die Gleichung auch keine quadratischen Glieder enthält, dann ist der Koordinatenursprung ein Dreifachpunkt.

Beispiel

Für die Lemniskate z.B. ergibt sich die Gleichung

Beispiel B
	von den Punkten (0,0), und liegt nur der erste auf der Kurve. Weiter ist d.h., der Koordinatenursprung ist ein isolierter Punkt.

Beispiel C
	Die Gleichungen liefern nur die eine Lösung (0,0), die auch die Gleichung erfüllt. Außerdem ist und so daß der Koordinatenursprung ein Rückkehrpunkt 2. Art ist, was auch aus der expliziten Form der Gleichung erkannt werden kann. Für ist nicht definiert, während für beide -Werte positiv sind; im Koordinatenursprung verläuft die Tangente horizontal.