Lemniskate
Lemniskate nennt man den Spezialfall 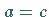 der CASSINIschen Kurven ,
die der Bedingung genügen
der CASSINIschen Kurven ,
die der Bedingung genügen
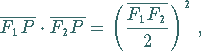 |
(2.229) |
wobei die Fixpunkte 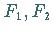 bei
bei 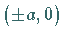 liegen.
Die Gleichung lautet in kartesischen und in Polarkoordinaten
liegen.
Die Gleichung lautet in kartesischen und in Polarkoordinaten
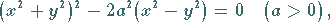 |
(2.230a) |
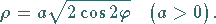 |
(2.230b) |
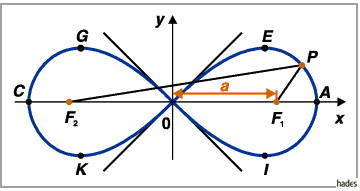
Der Koordinatenursprung ist Doppelpunkt und Wendepunkt zugleich, wobei die Tangenten
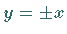 sind.
sind.
Die Schnittpunkte  und
und 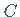 mit der
mit der  -Achse liegen bei
-Achse liegen bei
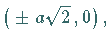 die Maxima und Minima
die Maxima und Minima 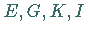 bei
bei
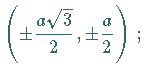 der Polarwinkel beträgt
in diesen Punkten
der Polarwinkel beträgt
in diesen Punkten 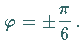
Der Krümmungsradius ergibt sich zu 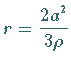 und der
Flächeninhalt jeder Schleife zu
und der
Flächeninhalt jeder Schleife zu 
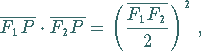
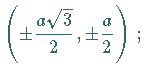 der Polarwinkel beträgt
in diesen Punkten
der Polarwinkel beträgt
in diesen Punkten 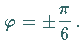
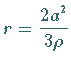 und der
Flächeninhalt jeder Schleife zu
und der
Flächeninhalt jeder Schleife zu