Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Gleichung einer Kurve

Jeder Gleichung 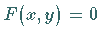für die Koordinaten 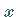und 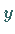entspricht eine Kurve, die die Eigenschaft hat, daß die Koordinaten jedes beliebigen Kurvenpunktes der Gleichung genügen und daß umgekehrt jeder Punkt, dessen Koordinaten diese Gleichung erfüllen, auf der Kurve liegt. Die Menge dieser Punkte wird auch geometrischer Ort genannt. Wenn die Gleichung 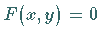von keinem reellen Punkt der Ebene erfüllt wird, dann gibt es keine reelle Kurve; man spricht von einer imaginären Kurve .
Man spricht von einer algebraischen Kurve 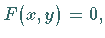wenn 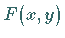ein Polynom ist, und nennt seinen Grad die Ordnung der Kurve. Wenn die Gleichung der Kurve nicht auf die Form 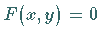mit 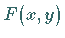als Polynom gebracht werden kann, dann spricht man von einer transzendenten Kurve .
Die Gleichungen von Kurven in anderen Koordinatensystemen können in analoger Weise betrachtet werden. Im weiteren werden aber, falls nicht ausdrücklich darauf hingewiesen wird, nur die kartesischen Koordinaten verwendet.

Beispiel A

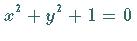: algebraische Kurve,

Beispiel B

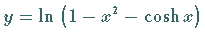: transzendente Kurve.