|
|
|
|
entweder 
oder 
geht.
 |
(3.478a) |
b) Die Asymptote ist eine vertikale Gerade:
 |
(3.478b) |
c) Die Asymptote ist eine Gerade mit
: Wenn sowohl
als auch 
gegen unendlich gehen, dann sind die Grenzwerte
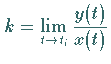und
zu bilden.
Existieren sie beide, dann liefern sie die Konstanten für die Geradengleichung der
Asymptote:
 |
(3.478c) |
| Beispiel | |
|
| |
ermittelt, die horizontalen und geneigten Asymptoten als Gerade mit den
entsprechenden Grenzwerten:
 |
(3.479) |
ist ein Polynom in 
und 
.
Für horizontale und vertikale Asymptoten einerseits und geneigte Asymptoten
andererseits ist je ein anderes Verfahren notwendig.
und 
die Glieder
mit dem höchsten Grad 
ausgewählt, als Funktion 
abgespaltet und nach
und
aufgelöst:
 |
(3.480) |
Die Werte 
für 
ergeben die horizontalen Asymptoten
die Werte 
für 
die vertikalen 
2. Asymptoten mit der Geradengleichung:
Zur Bestimmung der geneigten Asymptoten mit der Gleichung 
wird in
die Geradengleichung
eingesetzt und das so gewonnene Polynom
nach Potenzen von
geordnet:
 |
(3.481) |
Die Parameter 
und 
ergeben sich, falls sie existieren, aus den Gleichungen
 |
(3.482) |
| Beispiel | |
|
Betrachtung des kartesischen Blattes mit Aus den Gleichungen 
und
ergeben sich die Lösungen 
so daß sich die
Gleichung der Asymptote zu 
ergibt.
| |
|
|
Für die zweite Asymptote usw. erhält man in Analogie dazu
