|
|
|
|
| (3.380) |
| (3.381b) |
| In bezug auf die alten Achsen |
Richtungskosinus
der neuen Achsen |
||
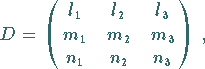 |
(3.381c) |
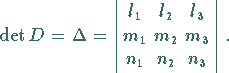 |
(3.381d) |
| (3.382a) |
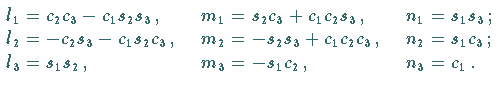 |
(3.382b) |
| Beispiel A | |
|
Die Komponenten eines Vektors | |
| Beispiel B | |
|
Die Länge des Vektors | |
| Beispiel C | |
|
Das Skalarprodukt eines Vektors mit sich selbst ist eine
skalare Invariante:
| |
|
|
|