Affine Koordinaten
Affine Koordinaten sind eine Verallgemeinerung der kartesischen Koordinaten auf ein
System aus drei linear unabhängigen, also auch nicht mehr zwingend rechtwinklig
aufeinander stehenden nichtkomplanaren Grundvektoren
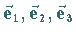mit drei Koeffizienten 
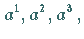wobei die oberen Indizes keinesfalls als Exponenten aufzufassen sind.
In Analogie zu (3.263a,b) ergibt sich 
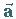zu
 |
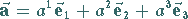(3.267a) |
oder
 |
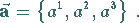(3.267b) |
Diese Schreibweise ist insofern vorteilhaft, als die Skalare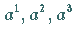 
die
kontravarianten Koordinaten eines Vektors sind.
Für 
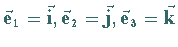gehen die Formeln (3.267a,b) in (3.263a,b) über.
Für die Linearkombination der Vektoren (3.260b) sowie für die Summe und die
Differenz zweier Vektoren (3.265a,b) gelten in Analogie zu (3.264) die
Komponentengleichungen
 |
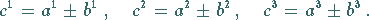(3.268b) |
