|
|
|
|
| (19.89a) |
oder
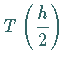 gemäß (19.89b)
und betrachtet die Linearkombination
gemäß (19.89b)
und betrachtet die Linearkombination
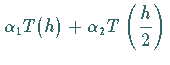 |
|||
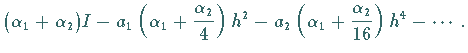 |
(19.90) |
Setzt man ![]() und
und 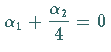 ,
dann
hat
,
dann
hat ![]() die Fehlerordnung 4, während
die Fehlerordnung 4, während ![]() und
und ![]() beide nur die
Fehlerordnung 2 haben.
Es ergibt sich
beide nur die
Fehlerordnung 2 haben.
Es ergibt sich
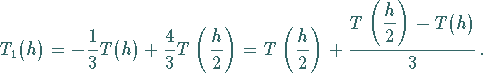 |
(19.91) |
| Beispiel | |
|
Für das bestimmte Integral  2. Trapez- und Simpson-Formel: Aus dem Schema zum ROMBERG-Verfahren liest man unmittelbar ab, daß für Die Verbesserung der Trapezformel nach HERMITE gemäß (19.77) liefert 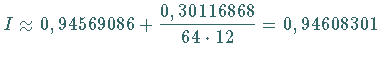 . .
3. Gauß-Formel: Nach Formel (19.83) erhält man für 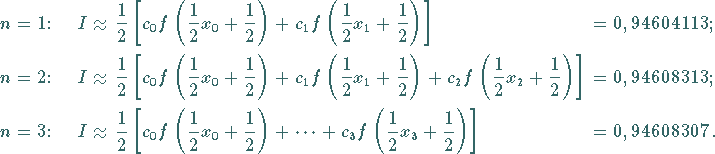
| |
Hinweise:
1. Eigenständige Bedeutung hat die Integration periodischer Funktionen im
Zusammenhang mit der FOURIER-Analyse erlangt.
Ihre numerische Realisierung findet man unter dem Stichwort
Harmonische Analyse, die auf dem Rechner mit Hilfe der sogenannten
Schnellen FOURIER-Transformation FFT
(Fast FOURIER Transformation) durchgeführt wird.
2. In vielen Fällen ist es zweckmäßig, bei der numerischen Integration
spezielle Eigenschaften des Integranden auszunutzen.
Auf diese Weise sind neben den oben vorgestellten Quadraturformeln noch viele andere
entwickelt worden, und die Literatur zu Fragen der Konvergenz, der Abschätzung des
Quadraturformelfehlers oder zur Konstruktion optimaler Quadraturformeln ist sehr
umfangreich (s. Lit. 19.3).
3. Zur numerischen Integration mehrfacher Integrale muß auf die Literatur
verwiesen werden (s. Lit. 19.30).
|
|
|