Setzt man in (19.81) als Integrationsintervall 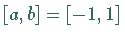 ,
und
wählt man als Stützstellen die Nullstellen der
LEGENDREschen Polynome (s. auch Tabelle
LEGENDREsche Polynome)
, dann können die Koeffizienten
,
und
wählt man als Stützstellen die Nullstellen der
LEGENDREschen Polynome (s. auch Tabelle
LEGENDREsche Polynome)
, dann können die Koeffizienten 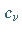 so bestimmt werden,
daß die Formel (19.81) Polynome bis zum Grad
so bestimmt werden,
daß die Formel (19.81) Polynome bis zum Grad 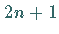 exakt integriert.
Die Nullstellen der LEGENDREschen Polynome liegen symmetrisch zum Nullpunkt.
Für die Fälle
exakt integriert.
Die Nullstellen der LEGENDREschen Polynome liegen symmetrisch zum Nullpunkt.
Für die Fälle 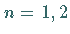 und 3 erhält man:
und 3 erhält man:
 |
(19.82) |
Hinweis: Durch die Transformation 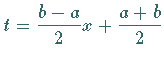 läßt sich das allgemeine Integrationsintervall auf das Intervall
läßt sich das allgemeine Integrationsintervall auf das Intervall 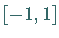 transformieren.
Mit den obigen für das Intervall
transformieren.
Mit den obigen für das Intervall 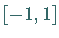 gültigen Werten für
gültigen Werten für 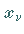 und
und 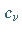 gilt dann:
gilt dann:
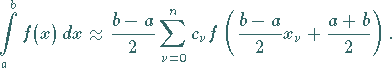 |
(19.83) |

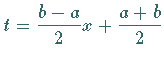 läßt sich das allgemeine Integrationsintervall auf das Intervall
läßt sich das allgemeine Integrationsintervall auf das Intervall ![]() transformieren.
Mit den obigen für das Intervall
transformieren.
Mit den obigen für das Intervall ![]() gültigen Werten für
gültigen Werten für ![]() und
und ![]() gilt dann:
gilt dann: