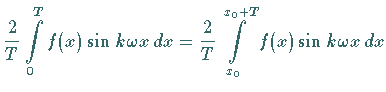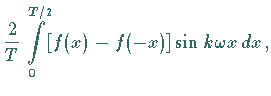Fourier-Darstellung periodischer Funktionen (Fourier-Analyse)
Oft ist es notwendig oder vorteilhaft, eine gegebene periodische Funktion 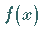 mit der
Periode
mit der
Periode 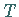 exakt oder angenähert durch eine Summe aus trigonometrischen Funktionen in
der Form
exakt oder angenähert durch eine Summe aus trigonometrischen Funktionen in
der Form
darzustellen.
Man spricht von FOURIER-Entwicklung .
Dabei gilt für die Kreisfrequenz 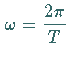 .
Im Falle
.
Im Falle 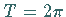 ist
ist  .
Die beste Approximation von
.
Die beste Approximation von 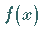 in dem unter ,,Wichtigste Eigenschaften von
FOURIER-Reihen`` angegebenen Sinne erreicht man mit einer
Näherungsfunktion
in dem unter ,,Wichtigste Eigenschaften von
FOURIER-Reihen`` angegebenen Sinne erreicht man mit einer
Näherungsfunktion 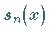 ,
wenn für die Koeffizienten
,
wenn für die Koeffizienten 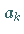 und
und 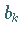 mit
mit
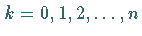 die FOURIER-Koeffizienten der gegebenen Funktion gewählt
werden.
Ihre Bestimmung geschieht analytisch mit Hilfe der EULERschen Formeln
die FOURIER-Koeffizienten der gegebenen Funktion gewählt
werden.
Ihre Bestimmung geschieht analytisch mit Hilfe der EULERschen Formeln
und
oder näherungsweise mit Hilfe der harmonischen Analyse.
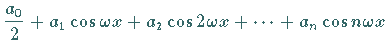
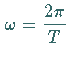 .
Im Falle
.
Im Falle