Verfahren für unrestringierte Aufgaben
Es wird das allgemeine Optimierungsproblem
 |
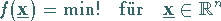(18.71) |
mit einer stetig differenzierbaren Funktion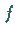 
betrachtet.
Mit den in diesem Abschnitt beschriebenen Verfahren wird eine im allgemeinen unendliche
Punktfolge 
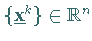konstruiert, deren Häufungspunkte stationäre
Punkte sind.
Die Punktfolge wird ausgehend von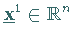 
nach der Vorschrift
 |
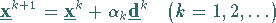(18.72) |
berechnet, d.h., in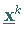 
wird eine Richtung 
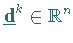bestimmt
und mittels des Schrittweitenparameters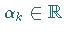 
festgelegt,
wie weit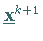 
in Richtung 
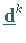von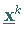
entfernt liegt.
Ein so konstruiertes Verfahren heißt Abstiegsverfahren , wenn gilt
 |
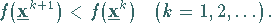(18.73) |
Die Bedingung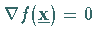 
,
wobei 
der Nablaoperator
ist, charakterisiert einen stationären Punkt und kann als Abbruchtest für die
Iterationsverfahren herangezogen werden.
