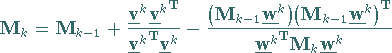Verfahren von Davidon, Fletcher und Powell (DFP)
Mit dem DFP-Verfahren ermittelt man, ausgehend von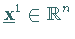 
,
eine Punktfolge nach der Vorschrift
 |
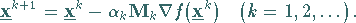(18.83) |
Dabei ist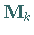 
eine symmetrische, positiv definite Matrix.
Die Idee des Verfahrens besteht in einer schrittweisen Approximation der inversen
HESSE-Matrix durch die Matrizen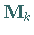
in dem
Falle, daß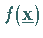 
eine quadratische Funktion ist.
Ausgehend von einer symmetrischen, positiv definiten Matrix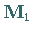 
,
z.B.
(
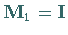Einheitsmatrix), wird
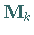aus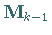 
durch Addition einer Rang-Zwei-Korrekturmatrix
 |
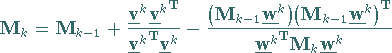(18.84) |
mit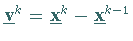 
und
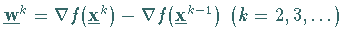ermittelt.
Die Schrittweite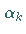 
erhält man durch Strahlminimierung aus
 |
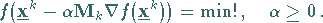(18.85) |
Ist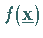
eine quadratische Funktion, dann geht das DFP-Verfahren für
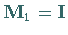in das Verfahren der konjugierten Gradienten über.
