Nablaoperator
Nablaoperator wird ein symbolischer Vektor 
genannt, der häufig zur
Darstellung von räumlichen Differentialoperationen benutzt wird und dessen Einführung
Berechnungen in der Vektoranalysis vereinfacht.
Für die Operatoren Gradient, Vektorgradient, Divergenz und Rotation gelten die
folgenden Formeln:
Gradient von
 |
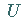
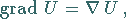(13.65a) |
Vektorgradient von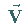
 |
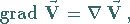(13.65b) |
Divergenz von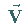
 |
(13.65c) |
Rotation von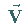
 |
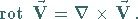(13.65d) |
In kartesischen Koordinaten gilt:
 |
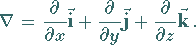(13.65e) |
Die Komponenten des Nablaoperators sind als partielle Ableitungsoperatoren aufzufassen,
d.h., das Symbol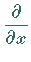 
schreibt die partielle Ableitung nach
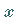vor, wobei die anderen Variablen als Konstanten betrachtet werden.
Die Formeln für die räumlichen Differentialoperatoren in kartesischen Koordinaten
ergeben sich durch formale Multiplikation dieses Vektoroperators mit dem Skalar 
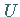oder
dem Vektor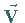 
.
