Verfahren der konjugierten Gradienten
Zwei Vektoren 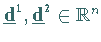 heißen konjugierte Vektoren
bezüglich einer symmetrischen, positiv definiten Matrix
heißen konjugierte Vektoren
bezüglich einer symmetrischen, positiv definiten Matrix 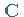 ,
wenn gilt
,
wenn gilt
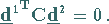 |
(18.80) |
Sind 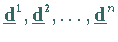 paarweise konjugierte Vektoren
bezüglich einer Matrix
paarweise konjugierte Vektoren
bezüglich einer Matrix  ,
dann ist das konvexe quadratische Problem
,
dann ist das konvexe quadratische Problem
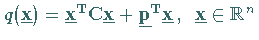 ,
in
,
in 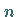 Schritten lösbar, wenn ausgehend von einem beliebigen
Schritten lösbar, wenn ausgehend von einem beliebigen
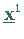 die Folge
die Folge 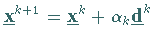 gebildet wird,
wobei
gebildet wird,
wobei 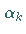 als optimale Schrittweite in Abstiegsrichtung gewählt wird.
Unter der Annahme, daß
als optimale Schrittweite in Abstiegsrichtung gewählt wird.
Unter der Annahme, daß 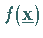 in der Nähe des Minimalpunktes
in der Nähe des Minimalpunktes 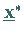 annähernd quadratisch ist, d.h.
annähernd quadratisch ist, d.h.
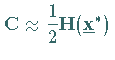 ,
kann das für quadratische
Zielfunktionen resultierende Verfahren auch auf allgemeinere Funktionen
,
kann das für quadratische
Zielfunktionen resultierende Verfahren auch auf allgemeinere Funktionen 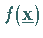 angewendet werden, ohne daß dabei explizit die Matrix
angewendet werden, ohne daß dabei explizit die Matrix  benutzt wird.
benutzt wird.
Das Verfahren der konjugierten Gradienten besteht aus folgenden Schritten:
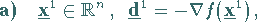 |
(18.81) |
wobei 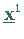 eine geeignete Ausgangsnäherung für
eine geeignete Ausgangsnäherung für 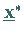 ist.
ist.
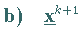 |
 |
 |
(18.82a) |
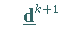 |
 |
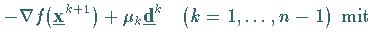 |
(18.82b) |
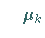 |
 |
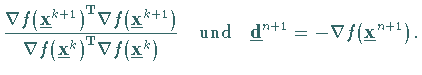 |
(18.82c) |
c) Wiederholung des Schrittes b) mit 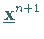 und
und
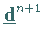 an Stelle von
an Stelle von 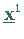 und
und 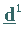 .
.
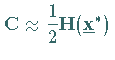 ,
kann das für quadratische
Zielfunktionen resultierende Verfahren auch auf allgemeinere Funktionen
,
kann das für quadratische
Zielfunktionen resultierende Verfahren auch auf allgemeinere Funktionen