Minimumsuche im n-dimensionalen euklidischen Vektorraum
Die Suche nach einer Näherung für einen Minimalpunkt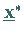 
des Problems
,
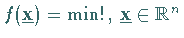kann auf die Lösung einer Folge
eindimensionaler Optimierungsprobleme zurückgeführt werden.
 |
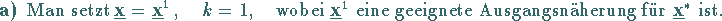(18.70a) |
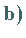Man löst für 
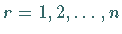die eindimensionalen
Probleme
 |
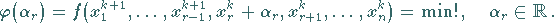(18.70b) |
Ist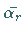 
ein Minimalpunkt bzw. eine Näherung des 
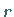-ten Problems, dann
setzt man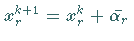 
.
Unterscheiden sich zwei aufeinander folgende Näherungen
hinreichend wenig, d.h. gilt für die Norm
 |
(18.70c) |
dann ist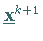 
eine Näherung für 
.
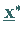Anderenfalls geht man mit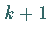 
an Stelle von 
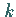zu Schritt b über.
Die eindimensionalen Probleme im Schritt b) können unter anderem auch mit den
unter Eindimensionale Suche beschriebenen Suchverfahren gelöst
werden.
