Anwendung des Newton-Verfahrens
Die Funktion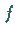 
wird im aktuellen Näherungspunkt 
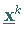durch eine quadratische
Funktion approximiert:
 |
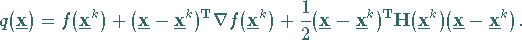(18.77) |
Dabei ist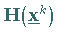 
die HESSE-Matrix, d.h. die Matrix der zweiten
partiellen Ableitung von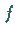
im Punkt 
.
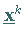Ist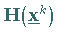
positiv definit, dann hat 
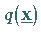an der Stelle
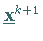mit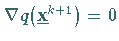 
ein globales Minimum, und man
erhält für das NEWTON-Verfahren die Iterationsvorschrift
Das NEWTON-Verfahren hat eine hohe Konvergenzgeschwindigkeit, der aber folgende
Nachteile gegenüberstehen:
a) Die Matrix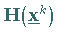
muß positiv definit sein.
b) Das Verfahren konvergiert nur für hinreichend gute Startwerte.
c) Es gibt keine Schrittweitensteuerung.
d) Das Verfahren ist im allgemeinen kein Abstiegsverfahren.
e) Der Aufwand zur Berechnung von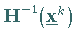 
ist mitunter recht
groß.
Einige Nachteile können durch die folgende Version eines gedämpften
NEWTON-Verfahrens behoben werden:
 |
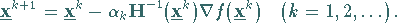(18.79) |
Der Dämpfungsfaktor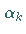 
kann unter anderem durch
Strahlminimierung ermittelt werden.
