Themen dieser Seite
Standardform einer Kreisabbildung
Die Abbildung 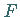 aus (17.80) ist für
aus (17.80) ist für 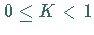 ein
orientierungstreuer Diffeomorphismus, da
ein
orientierungstreuer Diffeomorphismus, da
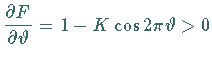 ist.
Bei
ist.
Bei 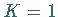 ist
ist 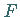 kein Diffeomorphismus mehr, aber noch ein Homöomorphismus,
während für
kein Diffeomorphismus mehr, aber noch ein Homöomorphismus,
während für 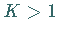 die Abbildung nicht mehr invertierbar und damit auch kein
Homöomorphismus mehr ist.
Im Parameterbereich
die Abbildung nicht mehr invertierbar und damit auch kein
Homöomorphismus mehr ist.
Im Parameterbereich 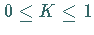 ist für
ist für 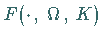 die
Rotationszahl
die
Rotationszahl 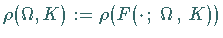 definiert.
Sei
definiert.
Sei 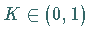 fixiert.
Dann hat
fixiert.
Dann hat 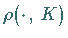 auf [0,1] folgende Eigenschaften:
auf [0,1] folgende Eigenschaften:
a) Die Funktion 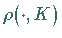 ist nicht fallend, stetig, aber nicht
differenzierbar.
ist nicht fallend, stetig, aber nicht
differenzierbar.
b) Für jede rationale Zahl 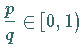 existiert ein Intervall
existiert ein Intervall
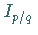 ,
dessen Inneres nicht leer ist und für das
,
dessen Inneres nicht leer ist und für das
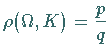 für alle
für alle 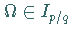 gilt.
gilt.
c) Für jede irrationale Zahl 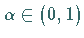 gibt es genau ein
gibt es genau ein  mit
mit
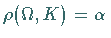 .
.
Teufelstreppe und Arnold-Zunge
Für jedes 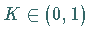 ist
ist 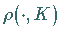 also eine CANTOR-Funktion.
Der Graph von
also eine CANTOR-Funktion.
Der Graph von 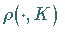 ,
der auf der rechten Abbildung gezeigt ist, heißt
Teufelstreppe (devil's staircase) .
,
der auf der rechten Abbildung gezeigt ist, heißt
Teufelstreppe (devil's staircase) .
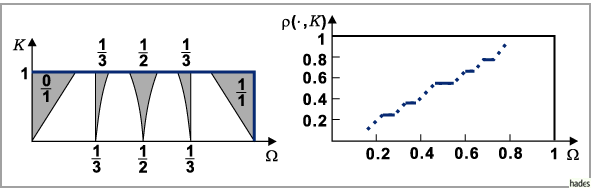
Das Bifurkationsdiagramm von (17.80) ist auf der linken Abbildung
zu sehen.
Von jeder rationalen Zahl auf der 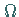 -Achse geht ein schnabelförmiges Gebiet
( ARNOLD- Zunge ) mit nicht leerem Inneren aus, in dem die Rotationszahl
konstant und gleich der rationalen Zahl ist.
Ursache für das Entstehen der Zungen ist eine Synchronisation der Frequenzen
( Frequenzkopplung (frequency locking)).
-Achse geht ein schnabelförmiges Gebiet
( ARNOLD- Zunge ) mit nicht leerem Inneren aus, in dem die Rotationszahl
konstant und gleich der rationalen Zahl ist.
Ursache für das Entstehen der Zungen ist eine Synchronisation der Frequenzen
( Frequenzkopplung (frequency locking)).
Für 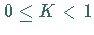 überlappen sich diese Gebiete nicht.
Von jeder irrationalen Zahl auf der
überlappen sich diese Gebiete nicht.
Von jeder irrationalen Zahl auf der 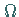 -Achse geht eine stetige Kurve aus, die
immer die Gerade
-Achse geht eine stetige Kurve aus, die
immer die Gerade 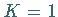 erreicht.
In der ersten ARNOLD-Zunge mit
erreicht.
In der ersten ARNOLD-Zunge mit 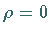 hat das dynamische System
(17.80) Ruhelagen.
Ist
hat das dynamische System
(17.80) Ruhelagen.
Ist 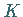 fixiert und wächst
fixiert und wächst 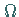 an, so verschmelzen auf dem Rand der ersten
ARNOLD-Zunge zwei dieser Ruhelagen und heben sich dabei gleichzeitig auf.
Im Ergebnis einer solchen Sattelknoten-Bifurkation entsteht ein auf
an, so verschmelzen auf dem Rand der ersten
ARNOLD-Zunge zwei dieser Ruhelagen und heben sich dabei gleichzeitig auf.
Im Ergebnis einer solchen Sattelknoten-Bifurkation entsteht ein auf 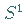 dichter Orbit.
Ähnliche Erscheinungen lassen sich beim Verlassen der anderen ARNOLD-Zungen
beobachten.
dichter Orbit.
Ähnliche Erscheinungen lassen sich beim Verlassen der anderen ARNOLD-Zungen
beobachten.
Für 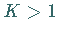 ist die Theorie der Rotationszahlen nicht mehr anwendbar.
Die Dynamik wird komplizierter, und es findet ein Übergang zum Chaos statt.
Dabei treten, ähnlich wie im Falle der
FEIGENBAUM-Konstante, weitere Konstanten auf, die für
bestimmte Klassen von Abbildungen, zu denen auch die Standardkreisabbildung gehört,
gleich sind.
Eine davon wird im folgenden beschrieben.
ist die Theorie der Rotationszahlen nicht mehr anwendbar.
Die Dynamik wird komplizierter, und es findet ein Übergang zum Chaos statt.
Dabei treten, ähnlich wie im Falle der
FEIGENBAUM-Konstante, weitere Konstanten auf, die für
bestimmte Klassen von Abbildungen, zu denen auch die Standardkreisabbildung gehört,
gleich sind.
Eine davon wird im folgenden beschrieben.
Die irrationale Zahl 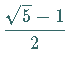 heißt Goldenes Mittel
und besitzt die einfache Kettenbruchdarstellung
heißt Goldenes Mittel
und besitzt die einfache Kettenbruchdarstellung
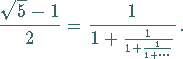 |
(17.84) |
Durch sukzessives Abschneiden des Kettenbruches erhält man eine Folge 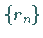 von
rationalen Zahlen, die gegen
von
rationalen Zahlen, die gegen 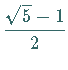 konvergiert.
Die Zahlen
konvergiert.
Die Zahlen 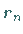 lassen sich in der Form
lassen sich in der Form 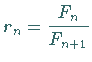 darstellen,
wobei
darstellen,
wobei 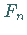 FIBONACCI-Zahlen sind, die sich
durch die Iterationsvorschrift
FIBONACCI-Zahlen sind, die sich
durch die Iterationsvorschrift
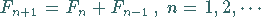 |
(17.85) |
mit den Startwerten 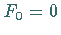 und
und 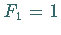 bestimmen lassen.
Sei nun
bestimmen lassen.
Sei nun 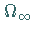 der Parameterwert von (17.80), für den
der Parameterwert von (17.80), für den
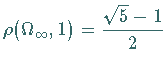 ist und sei jeweils
ist und sei jeweils 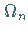 der
der
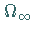 am nächsten liegende Wert, für den
am nächsten liegende Wert, für den 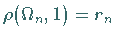 ist.
Eine numerische Analyse ergibt den Grenzwert
ist.
Eine numerische Analyse ergibt den Grenzwert
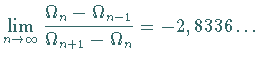 .
.
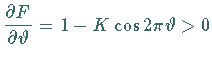 ist.
Bei
ist.
Bei 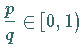 existiert ein Intervall
existiert ein Intervall
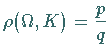 für alle
für alle ![]() ist die Theorie der Rotationszahlen nicht mehr anwendbar.
Die Dynamik wird komplizierter, und es findet ein Übergang zum Chaos statt.
Dabei treten, ähnlich wie im Falle der
FEIGENBAUM-Konstante, weitere Konstanten auf, die für
bestimmte Klassen von Abbildungen, zu denen auch die Standardkreisabbildung gehört,
gleich sind.
Eine davon wird im folgenden beschrieben.
ist die Theorie der Rotationszahlen nicht mehr anwendbar.
Die Dynamik wird komplizierter, und es findet ein Übergang zum Chaos statt.
Dabei treten, ähnlich wie im Falle der
FEIGENBAUM-Konstante, weitere Konstanten auf, die für
bestimmte Klassen von Abbildungen, zu denen auch die Standardkreisabbildung gehört,
gleich sind.
Eine davon wird im folgenden beschrieben.
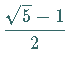 heißt Goldenes Mittel
und besitzt die einfache Kettenbruchdarstellung
heißt Goldenes Mittel
und besitzt die einfache Kettenbruchdarstellung
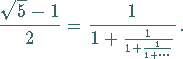
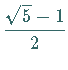 konvergiert.
Die Zahlen
konvergiert.
Die Zahlen 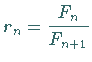 darstellen,
wobei
darstellen,
wobei 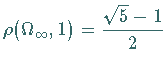 ist und sei jeweils
ist und sei jeweils 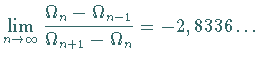 .
.