|
|
|
|
| Beispiel | |
|
Sind | |
| (17.79) |
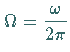 überführen.
Mit
überführen.
Mit 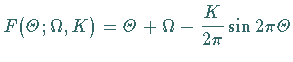 liegt eine äquivariante Abbildung vor, die die Standardform der Kreisabbildung
erzeugt.
liegt eine äquivariante Abbildung vor, die die Standardform der Kreisabbildung
erzeugt.
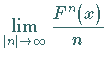 ,
und
dieser Grenzwert hängt nicht von
,
und
dieser Grenzwert hängt nicht von 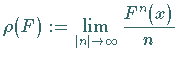 definiert werden.
Ist
definiert werden.
Ist
Ist ![]() in (17.78) ein orientierungstreuer
Homöomorphismus, so hat die Rotationszahl folgende Eigenschaften
(s. Lit. 17.12):
in (17.78) ein orientierungstreuer
Homöomorphismus, so hat die Rotationszahl folgende Eigenschaften
(s. Lit. 17.12):
a) Hat (17.78) einen ![]() -periodischen Orbit, so existiert eine ganze
Zahl
-periodischen Orbit, so existiert eine ganze
Zahl ![]() ,
so daß
,
so daß 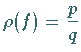 ist.
ist.
b) Ist ![]() ,
so hat (17.78) eine Ruhelage.
,
so hat (17.78) eine Ruhelage.
c) Ist 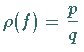 ,
wobei
,
wobei ![]() ,
ganzzahlig und
,
ganzzahlig und ![]() eine
natürliche Zahl ist (
eine
natürliche Zahl ist (![]() und
und ![]() teilerfremd), so hat (17.78) einen
teilerfremd), so hat (17.78) einen
![]() -periodischen Orbit.
-periodischen Orbit.
d) ![]() ist genau dann irrational, wenn (17.78) weder einen
periodischen Orbit noch eine Ruhelage besitzt.
ist genau dann irrational, wenn (17.78) weder einen
periodischen Orbit noch eine Ruhelage besitzt.
Satz von Denjoy:
Ist ![]() ein orientierungstreuer
ein orientierungstreuer ![]() -Diffeomorphismus und ist
die Rotationszahl
-Diffeomorphismus und ist
die Rotationszahl ![]() irrational, so ist
irrational, so ist ![]() topologisch konjugiert zu
einer reinen Drehung, deren geliftete Abbildung
topologisch konjugiert zu
einer reinen Drehung, deren geliftete Abbildung ![]() lautet.
lautet.
|
|
|